Skip to content

第八章 非线性控制系统分析

1 上课笔记

EXAM NOTIFICATION
填空选择非线性控制系统的特征 3 点：

  • 稳定性/输出瞬态响应：与输入信号和初始条件有关（这条可能会考）
    1. 系统输出的瞬态过程曲线形状与输入信号大小和系统初始条件有关。
    2. 系统的稳定性也与输入信号大小和初始条件有关。
  • 自激振荡
  • 频率响应发生畸变

需要记得公式不考

5 分大题描述函数法
把课本/课件上的例题好好看看就可以了！
判断交点处自激振荡的稳定性，求交点处频率与幅值.
只考简单的概念，没有复杂的计算.

线性系统与非线性系统

线性系统只是在特定条件下的近似描述
能否应用叠加定理是线性系统与非线性系统的本质区别。

稳定性分析复杂: 无外力作用，且系统输出各阶导数为 0 时，系统处于平衡状态.
线性系统只有一个平衡点 y=0
非线性系统可能有多个平衡点，只不过可能是不稳定的平衡点.
可能存在自激振荡现象
频率响应发生畸变: 输出存在高次谐波（分频？)

非线性类型：

  • 饱和：设计得当可以使超调量小且稳态误差小
  • 死区特性：系统存在稳态误差（稳态特性）, 降低了系统的跟踪精度（动态特性）, 减小扰动信号影响
  • 滞环/间隙特性：相当于死区，降低跟踪精度. 运动变化更加剧烈，不利于稳定性.
  • 继电特性：往往使系统产生震荡
    • 继电特性+滞环特性=非单值继电特性
    • 继电特性+死区特性=单值且有死区继电特性
    • a+b+c=非单值且有死区继电特性
  • 摩擦：低速运动不平滑性

非线性系统分析方法

  • 存在线性工作区域：线性化处理，线性分析再修正
    • 小偏差线性化法（系统方程解析且工作在某一数值附近的较小范围内）
    • 分段线性化法
    • 反馈线性化
  • 不存在线性工作区域
    • 描述函数法
    • 相平面法
    • （课本上还有一个逆系统法）

线性系统时域分析都是初始值为零，输入阶跃信号.
非线性系统往往初始值不为零，分析无输入（只有干扰）时的情况（或者理解为观察冲激响应？)

相平面法
\(\ddot{x}=f(x,\dot{x})\)
\(\ddot{x}=d\dot{x},\dot{x}=dx\)
\(\frac{d\dot{x}}{dx}=\frac{f(x,\dot{x})}{\dot{x}}\)

相平面图的绘制

  • 解析法
    • 直接积分获得\(f(x,\dot{x})=0\)相轨迹方程
    • 消除参变量法：消除 t
  • 图解法/作图法：等倾线法
  • 实验法

另外，如果分段解析的话，可分情况做出不同区域的相轨迹.

解析法思路总结：

  1. 根据\(\frac{d\dot{x}}{dx}=\frac{f(x,\dot{x})}{\dot{x}}\)积分可以获得\(f(x,\dot{x})=0\)曲线.

    对\(\dot{x}d\dot{x}=f(x,\dot{x})dx\) 进行积分时，需要注意\(x,\dot{x}\)都是时间的函数，左右同时积分时，积分上下限的确定：
    \(t:0\to t\)
    \(x(t):x(0)\to x(t)\)简写为\(x_0\to x\)
    \(\dot{x}(t):\dot{x}(0)\to \dot{x}(t)\)简写为\(\dot{x}_0\to \dot{x}\)

  2. 积分困难，可以分别求出\(x(t),\dot{x}(t)\), 消去 t 画曲线

  3. 如果还是难以消去 t, 就描点作图

相轨迹每一点切线处的斜率为：\(\frac{d\dot{x}}{dx}=\frac{f(x,\dot{x})}{\dot{x}}=\alpha\)

奇点：平衡点\(\frac{\ddot{x}}{\dot{x}}=\frac00\), 斜率不定
斜率不定，则相轨迹方向任意，说明这是各个相轨迹交汇处.
奇点有可能是发射点也有可能是收敛点。当奇点为收敛点时，代表了系统的稳定工作状态.

对线性系统来说，只有一个平衡状态——即对应一个奇点，
但对于非线性系统来说，可能有多个平衡状态，即对应多个奇点。
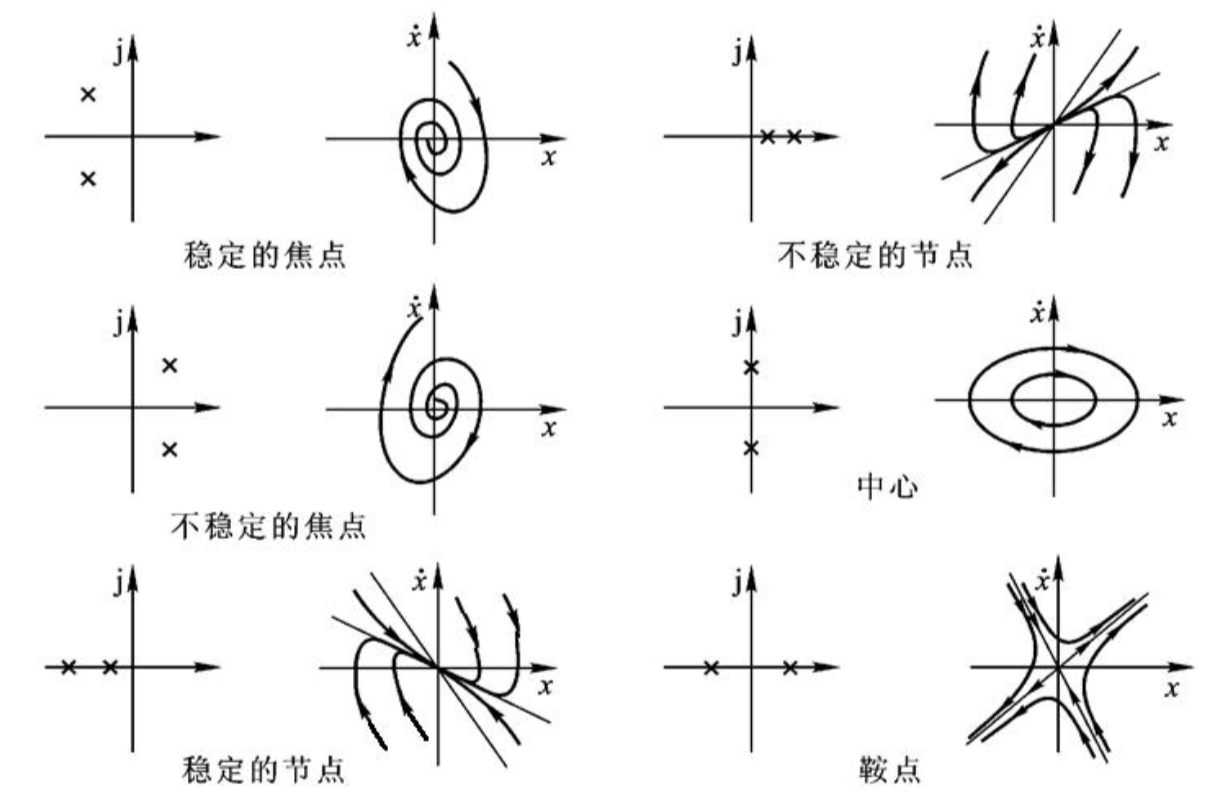
根据奇点附近相轨迹变化，奇点可分为稳定焦点、不稳定焦点、稳定节点、不稳定节点、中心点和鞍点

线性二阶系统的奇点分类：

  • 焦点
    • 震荡收敛（二阶欠阻尼）（负实部共轭复根）
    • 震荡发散（二阶负阻尼\(-1<\xi<0\))（正实部共轭复根）
  • 节点
    • 单调收敛（二阶过阻尼）（两个负实根）
    • 单调发散（二阶负阻尼\(\xi<-1\)>>)（两个正实根）
  • 中心点：到达不了（虚轴极点）
  • 鞍点（一个正实根，一个负实根）

奇点分类

等倾线法思路总结：

  • \(\frac{d\dot{x}}{dx}=\frac{f(x,\dot{x})}{\dot{x}}=\alpha\)画出的曲线上，如果相轨迹穿过这条曲线，那么穿越点处斜率一定为\(\alpha\)
  • 通过绘制等倾线，我们可以知道任意一个地方的相轨迹斜率
  • 等倾线法就是通过等倾曲线以及初始点，获得近似的相轨迹.
    • 例如我们从一个点\((x,\dot{x})\)出发
    • 先看这个点位置的斜率，以及接下来到达的等倾线的斜率
    • 两个斜率取平均作为从这个点出发的斜率
    • 这个点以平均斜率出发到达下一个等倾线
    • 重复上述步骤

极限环与自激振荡的稳定性：
当等倾线不是直线时，相轨迹可能到达一个闭合的环，代表了系统稳定的震荡.

极限环

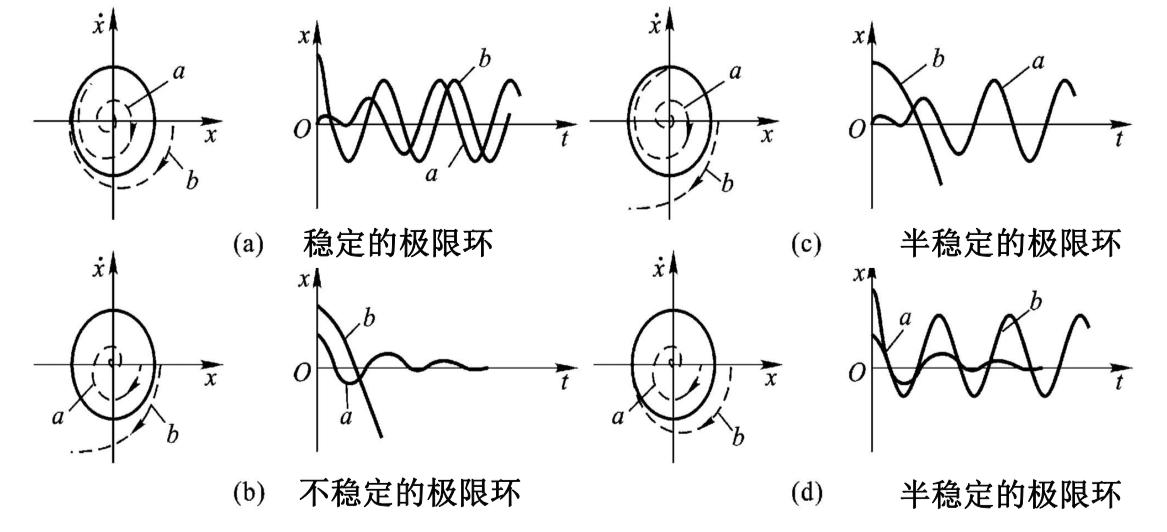
半稳定极限环是不会稳定震荡的，总是会有微小的扰动偏离极限环，最后发散或者回到奇点.

自激振荡的稳定性：假如说系统到达了自激振荡点，如果带来一个扰动，系统能稳定回归到自激振荡点.
与系统稳定性是不同的概念。

同理极限环的稳定性是指能够稳定产生自激振荡，而非系统稳定.

在描述函数法中，\(-\frac{1}{N(A)}\)与\(G(j\omega)\)存在交点则存在自激振荡点，通过扰动使震荡幅值增大/减小来判断工作点能否回到自激振荡点.

描述函数法

当系统满足一定的假设条件时，系统中非线性环节在正弦信号作用下的输出可用一次谐波（基波？) 分量来近似. 由此导出非线性环节的近似等效频率特性，即描述函数.
描述函数用来分析无外力作用的情况下，非线性系统的稳定性和自震荡问题.

  • 优点：不受系统阶次限制，可以分析频率特性
  • 缺点：系统首先得适合近似，不可以分析时域特性

描述函数不用背，考试会给，但是应该需要会分析.

MyOpinion:
将非线性环节合成一个部分,
并简化为一个不改变正弦信号频率, 只改变幅值和相位的
不随时间改变的描述函数.（相当于复数增益的放大器）
分析情况：无输入时的系统自激振荡现象，即研究对象是单一频率正弦波（不含直流分量）

综上，通过限制信号为正弦信号以及对非线性环节近似，将一个非线性系统简化为了"线性时不变系统"，并使用频率法进行分析.

  1. 系统结构一定是/一定能化成下述的形式.
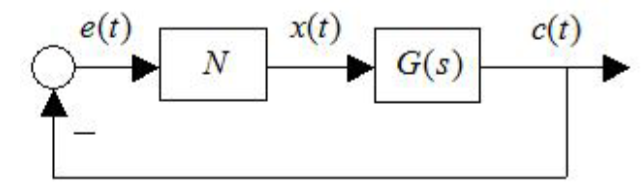
    系统结构
  2. 非线性部分的输入输出特性是不随时间改变的 x 的奇函数\(f(x)\), 或者正弦输入下的输出为 t 的奇对称函数\(y(t)\), 即输出不含直流分量，即非线性是对称的.
  3. 线性部分 G 需要较好地滤除高频（来自非线性环节，这样可以更好地拟合）
  4. 非线性元件只有一个正弦输入（系统自激振荡时，N 的输入也是正弦波）

系统结构化简方法小总结：
当系统框图结构不满足描述函数法要求的结构时，需要进行化简.

  • 利用相同特征方程进行化简：只是部分等效（传递函数极点相同）, 这样似乎只是判断稳定性（吧）
    • 求出\(\Phi(s)=\frac{C(s)}{R(s)}\), 模块使用 N,G 表示
    • 取特征方程，即\(\Phi(s)\)的分母
    • 化成\(1+NG'=0\)的形式，\(G'\)就是等效的
  • 利用信号传递关系等效变换
    MyOpinion:
    关键点有 N 的输入端 xe(t),N 的输出端 yx(t), 以及系统输出端 Cc(t)
    找到从 y 出发回到 x 的回路，这个回路上所有的线性模块合并为右图的G(s), 这样可以画出来一个单位负反馈的环了.
    因为上面为了凑出来单位负反馈，把原来反馈回路的给合并到G(s)里了，所以找到从 y 到达 C 的部分，在G(s)引出负反馈的端口右边再填上补偿环节，让 y 到达 C 的传函满足原本的关系.

描述函数\(N(A,j\omega)=\frac{\dot{X_1}}{\dot E}=\frac{B_1}{A}+j\frac{A_1}{A}\)
输出基波分量的复数相量/正弦输入的复数相量

  1. 输入正弦信号
  2. 获得输出信号（需要检验不含直流分量，含的话就不能用这个方法分析了）
  3. 获得基波分量正弦信号 求\(A_1,B_1,X_1,\varphi_1\)
  4. 获得描述函数\(N(A,j\omega)\)
    当非线性环节中不包含储能元件时，其输出的一次谐波分量的幅值和相位差与\(\omega\)无关，因此描述函数只是输入正弦信号幅值的函数\(N(A)\)
\[ \begin{aligned} x(t) & =\frac{A_{0}}{2}+\sum_{i=1}^{\infty}\left(A_{i} \cos i \omega t+B_{i} \sin i \omega t\right)\\ A_{0} & =\frac{1}{2 \pi} \int_{0}^{2 \pi} x(t) d(\omega t) \quad A_{0}\text{是直流分量} \\ A_{i} & =\frac{1}{\pi} \int_{0}^{2 \pi} x(t) \cos i \omega t d(\omega t) \quad i=0,1,2, \cdots \\ B_{i} & =\frac{1}{\pi} \int_{0}^{2 \pi} x(t) \sin i \omega t d(\omega t) \quad i=1,2,3, \cdots \\ Y_n & =\sqrt{A_n^2+B_n^2}\\ \varphi_n & =\arctan\frac{A_n}{B_n}\\ \end{aligned} \]

这里的\(x(t)\)是非线性环节的稳态输出.

非线性系统简化

  • 并联：描述函数线性相加
  • 串联：图解法化简（有点像高中学的复合函数）

描述函数法分析非线性系统稳定性
（描述函数分析非线性系统自激振荡）

  1. 实际是线性系统频域分析方法的扩展，复杂程度依次为：
  2. 线性系统恒定增益：一个点-1
  3. 线性系统变增益：\(-\frac{1}{K_1}\to-\frac{1}{K_2}\)
  4. 线性系统复数增益（描述函数）:\(-\frac{1}{N|_{A=0}}\to-\frac{1}{N|_{A=\infty}}\)
  5. 下述方法只适用于\(G(s)\)不具有右极点的情况，如果\(G(s)\)具有低通特性，则\(G(s)\)应当不具有右极点.

系统特征方式\(1+N(A)G(j\omega)=0\)
之前看 Nyquist 曲线与-1 点之间的关系判断稳定性.
现在看 Nyquist 曲线与曲线\(-\frac{1}{N(A)}\)的关系

MyOpinion: 之前是固定了一个点，看奈氏曲线是否包围这个点 (-1,0) 判稳. 现在是一个点集，对于每一个点，分别看奈氏曲线是否包围这个点.
当曲线包围点 P 时，系统不稳定，幅值将增大.
当曲线不包围点 P 时，系统稳定，幅值将减小.
当曲线穿过点 P 时，系统临界稳定，处于等幅振荡状态.

  • 奈氏曲线 A（此处记为曲线\(\Gamma_G\)) 不包围负倒描述函数曲线 B（此处记为曲线\(\Gamma_N\)), 系统总是稳定
  • A 包围 B, 系统总是不稳定
  • A 与 B 有交点，交点处是系统周期运动的点，\(G(j\omega)\)确定频率，\(-\frac{1}{N(A)}\)确定幅值.

    计算方法之一：实部对应相等，虚部对应相等

判断周期运动是否稳定（是否是稳定的自激振荡点）:

  • 给一个小扰动
  • 交点 P 移动到点 Q
  • 看点 Q 是否被奈氏曲线包围，判断稳定性
    • 不稳定，震荡幅值将增大
    • 稳定，震荡幅值将减小
  • Q 点沿着负倒描述函数曲线幅值 A 增大的方向走，看看能不能回到 P 点

结论：
\(\Gamma_G\)包围区域是不稳定区域，不包围的区域是稳定区域，曲线上是等幅振荡的临界区域.
\(\Gamma_N\)与\(\Gamma_G\)相交时，如果沿着 A 增加的方向，从不稳定区域进入稳定区域，则交点处对应稳定的周期运动；从稳定区域进入不稳定区域，则交点处对应不稳定的周期运动.

Back to top