第四章 线性系统的根轨迹法

• 第四章 线性系统的根轨迹法
  • 1 概念
  • 2 根轨迹性质与绘制方法
    • 2.1 绘制根轨迹的基本法则 x8
    • 2.2 补充说明
  • 3 根轨迹分析系统性能
    • 3.1 计算分离点
    • 3.2 由根轨迹获得闭环传递函数
      • 3.2.1 求闭环极点的方法
    • 3.3 开环传递函数存在零极点对消
    • 3.4 PID 对根轨迹影响分析
  • 4 广义根轨迹法
    • 4.1 参数根轨迹
    • 4.2 零度根轨迹
  • 5 上课笔记

写在前面

MATLAB 可以精确绘制根轨迹，手绘的意义在于理解根的变化规律.
所以重点应该在于理解不同操作对根轨迹的影响，而非手绘复杂根轨迹（需要一定的经验）.

1 概念

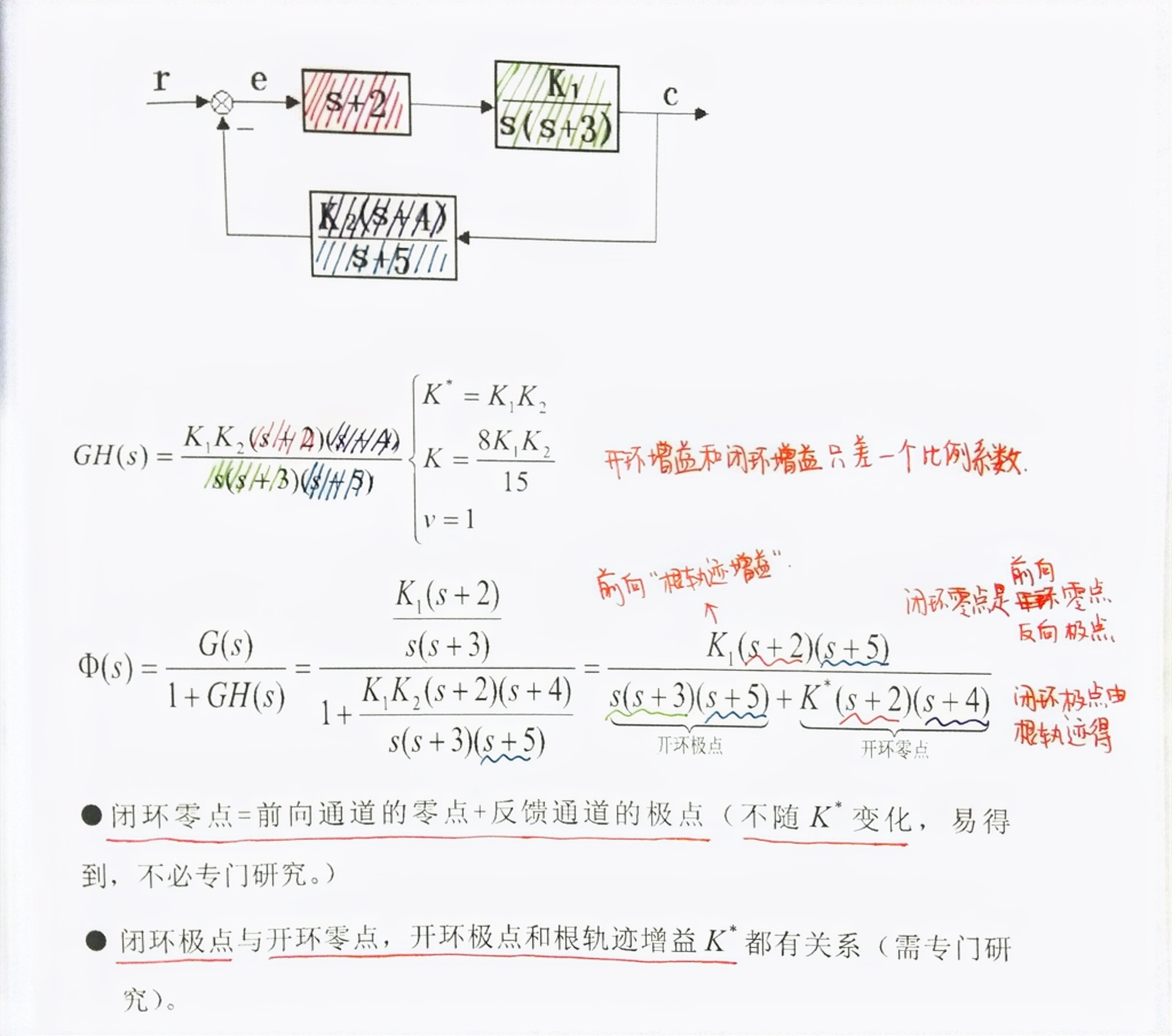
分母 = 0 即 \(1+G(s)=0\) 即为根轨迹方程.

注意区分根轨迹增益，开环增益

• 根轨迹增益 \(1+K^*G=0\) (G 必须要写成首一式）
  • 首一式即 s 的系数为 1, 比如说 \((-s+1)\to-(s-1)\), 还有\(s^n+...\)
  • 参数根轨迹下，要把变化的参数化成 根轨迹增益
  • 根轨迹增益从 0 到无穷大，画出根轨迹.
• 开环增益 \(G(s)\)
  • 闭环系统性能 \(e_{ss}=\frac AK\) , 分母是开环增益.

2 根轨迹性质与绘制方法

• 相角条件：\(\sum_{j=1}^{m}\angle\left(s-z_{j}\right)-\sum_{i=1}^{n}\angle\left(s-p_{i}\right)=(2k+1)\pi\quad(k=0,\pm1..)\)
  确定根轨迹，一般等式右边取 \(-180^\circ\) 时更好算
• 模值条件：\(K^{*}=\frac{\prod_{i=1}^{n}\left|s-p_{i}\right|}{\prod_{j=1}^{m}\left|s-z_{j}\right|}\)
  确定参数 K

一个点，满足相角条件（充要条件）一定在根轨迹上，
一个点，无论在不在根轨迹上，都能通过模值条件（必要条件）确定一个 K

对称性： （与奈式曲线区分）

• 根轨迹：K 0→∞, 180 度根轨迹；K 0→-∞, 0 度根轨迹. 两段根轨迹并不对称.
  但根轨迹关于实轴对称 （如果有复数极点，必定共轭）
  另外有一定理：开环零极点均为偶数且对称分布于某纵轴（平行于虚轴的直线）左右，则根轨迹对该纵轴对称
• 奈式曲线：\(\omega=0\to\infty\), 和 \(\omega=0\to-\infty\) 关于极轴对称

根之和与根之积

根之和: 闭环系统极点之和等于开环系统极点之和且为常数
根之积：

2.1 绘制根轨迹的基本法则 x8

画根轨迹前，列出开环传递函数，写出开环增益 K 的表达式，和系统型别。

🌟起点和终点：根轨迹起始于开环极点，终止于开环零点；
如果开环零点个数 m 少于开环极点个数 n ，则有 (n-m) 条根轨迹终止于无穷远处（广义零点）。
如果开环零点个数 m 大于开环极点个数 n ，则有 (m-n) 条根轨迹起始于无穷远处（广义极点）。（现实系统是因果系统，该情况只会出现理论分析中）

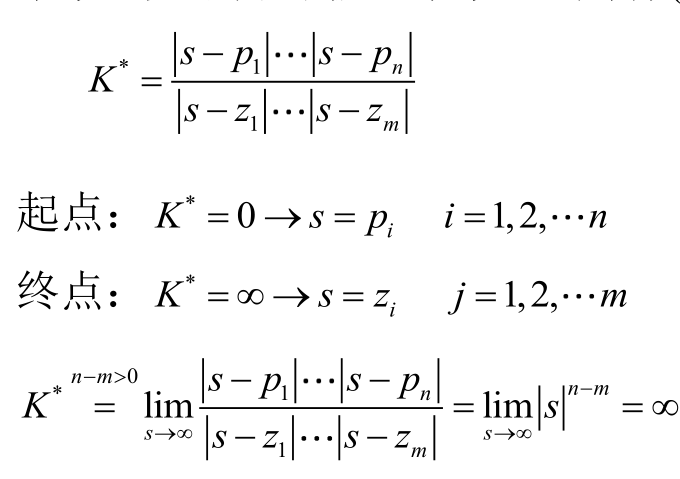
🌟根轨迹的分支数及对称性：分支数 = \(D(s)\) 阶数 = \(max(m, n)\) = 特征根个数
一般情况下，开环传函 \(G(s)\) 分母阶数 n 更高，所以分支数即为极点数.

🌟实轴上的根轨迹：从实轴最右端的开环零极点算起，奇数开环零极点到偶数开环零极点间一定是根轨迹，否则一定不是.

复数极点两两共轭，不影响实轴上极点的相角条件
如果是零度根轨迹，则从实轴最右端的无穷远点算起

Note

定理：当开环极点有 2 个，开环零点有 1 个，并且在复平面上有根轨迹时，则复平面上的根轨迹一定是以零点为圆心的圆弧。

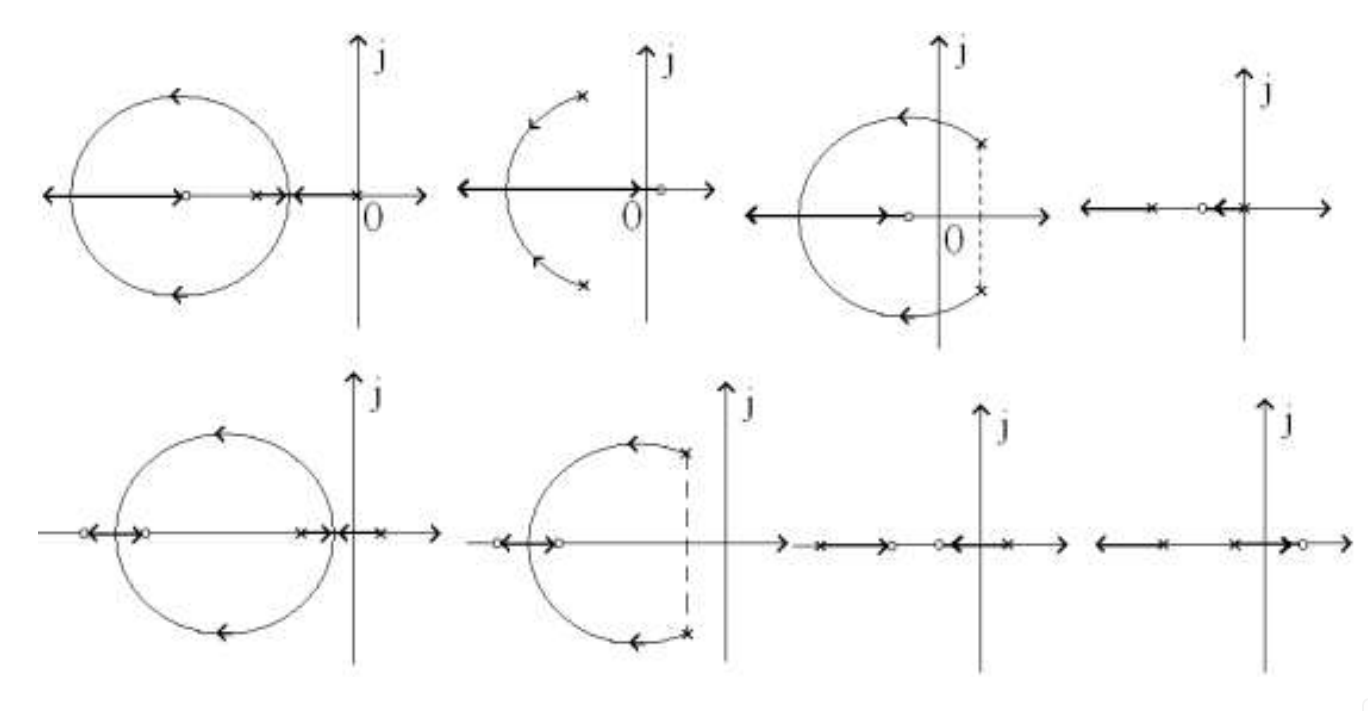
绘制根轨迹有一定的经验加成，形成感性理解（例如根要向零点走，零点就像提供了引力一样，根轨迹就变成了圆弧；还比如几个极点相会互相排斥，要按照最佳的方式分开，即均匀分配这 360°）, 根轨迹该怎么走就能猜个大概.

🌟根之和（注意适用条件）

• 作用一：定性判断根轨迹变化趋势，一部分极点往左移，必定有另一部分往右移，互相抵消
• 作用二：根据已知极点计算未知极点

🌟渐近线

卢京潮第 14 节课（上）有证明，通过跟轨迹方程.
"广义重心": s 位于无穷远点时，所有零极点对于 s 来说都是同一个位置，这个位置就是重心/质心 \(\sigma_i\)

🌟分离点坐标公式

计算分离点坐标方法有挺多，详见 分离点计算

🌟与虚轴的交点

• 带着根轨迹增益列劳斯表，让第一列临界稳定，即出现 0 , 即有出现与虚轴交点时 K 的值
• \(s=j\omega\) 位于根轨迹上，是根轨迹方程的根/特征根，则代入跟轨迹方程 \(D(s)=0\).
  等式要想成立，左边的实部和虚部都要为 0, 计算得到 \(\omega\)

🌟出射角，入射角

这个公式不用记，就理解为：出射/入射时，极点可视为与对应的极点/零点重合，在此基础上列相角条件即可.
还比如存在 3 重闭环极点，从此出射，在相角条件里就列上 \(3\theta\) 计算出射角
另外，相角条件的角度是从开环零极点指向根轨迹上的极点，在算入射角时要转换为根轨迹上极点指向开环零点.

2.2 补充说明

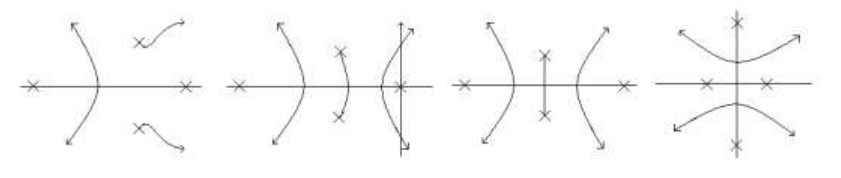
用以上法则，只能概略的画出根轨迹来（误差 20%)

开环零极点的位置有时略有变化，根轨迹可能有显著的不同，要依据情况具体分析而确定（关键在于分离点的确定）

3 根轨迹分析系统性能

1. 绘制根轨迹
2. 由根轨迹获得闭环传递函数
3. 保留主导极点，利用零点极点法分析系统性能 （其实还是用的时域分析方法）
   > 高阶系统说阻尼比，都是指的主导共轭极点

开环稳定性与闭环稳定性

开环稳定：开环极点都在左半平面
闭环稳定：闭环极点都在左半平面
开环稳定和闭环稳定没有关系，从根轨迹就可以理解.

• 负反馈未必能改善系统性能，只是提供了更多改善的机会 （根轨迹总体要往左偏）
• 正反馈增加系统发散的可能，但也有可能改善系统稳定性 （根轨迹总体往右偏）

3.1 计算分离点

核心原理：分离点处一定是根轨迹方程的重根 → 重根处一阶导数一定为 0

• 常规的 \(\sum \frac 1{d-p_i}=\sum \frac 1{d-z_j}\)...

需要注意，分子是一，分母是单根（复数根要拆开写）, 一边是零点，一边是极点. 没有零点写 0.

• \(M'N-N'M=0\) 感觉也挺方便的.
  （其实来源就是 \(1+G(s)\) 求导，就是 \(G'(s)=\frac{M'N-N'M}{N^2}\))

• 也可以直接 \(\frac{d}{ds}D(s)=0\)

Note

第一个方法是讲的最多的方法，虽然形式上比较麻烦，但是我想它的优势在于，方便用计算器进行试根.
用卡西欧计算器输入方程，根据根轨迹图像看一下分离点在哪个区间，然后设定初始值，就能试出来根.
我觉得其他方法则更适合手算，因为没有分数形式. 如果你手算第一个方法，会发现形式上会和第二个相同.

由于根轨迹特指 \(K^*=0\to \infty\) 的情况，因此计算出分离点后，要进行验证：

• 根据图像，明显不在根轨迹上就舍弃
• 由模值条件算出对应的\(K^*\), 为负数就舍弃

3.2 由根轨迹获得闭环传递函数

1. 闭环零点：前向通道零点，反馈通道极点
2. 闭环极点：对应 \(K^*\) 时，根轨迹上点的位置

3. 闭环增益：这个比较 tricky, 如果情况比较复杂就现推吧...

   反正记好特征方程的样子，如果 n>m 的化，特征方程是首一式 \(s^n+...\), 这样根据根轨迹读出极点，直接连乘就放到分母就好了.

   如果 n=m, 特征方程 \(N+KM\to (1+K)s^n+...\) 所以... （详细可以看 PPT （应该只适用于单位负反馈

总而言之，零极点是比较好看，闭环增益需要小心，没有特别方便的规律. 如果系统结构图已经给出来了，不妨手动去化，不会出错.

3.2.1 求闭环极点的方法

例如有时候会需要设计一个特定阻尼比的系统，这说明固定了角度，求射线和根轨迹的交点

• 根据特殊的几何关系（如根轨迹是圆，用相切，直角）
• 代数方法：根之和（与根之积）, 适用于只有一（两）个极点未知的情况
• 其他关系式，例如阻尼比已知，则设极点，代入相角条件.

3.3 开环传递函数存在零极点对消

• 画根轨迹时正常画（这个根轨迹阶数肯定是变低了对消次数的）
• 根轨迹只反映了随\(K^*\)变化的极点，同时还会存在不随之变化的极点
• 分析系统性能时，手动算一下闭环传递函数，找全所有闭环极点再进行分析

3.4 PID 对根轨迹影响分析

• P: 影响增益，如果比例部分为 1, 那么就不影响开环增益. 其他 PID 也是同样的.

• PD: 引入一个开环（实数）零点

  • 系统型别不变，P=1 时增益不变 → 稳态精度不变
  • 开环零点使根轨迹左移 → 极点左移 → 调节时间减小，超调量可以接受

• PI: 引入一个开环零点，同时引入一个积分环节 (\(s=0\)的开环极点）

  • 系统型别加 1, 稳态精度极大提高
  • 根轨迹新增一个从原点出发的极点，主导极点更有可能靠近虚轴 （应该可以这样理解吧...) → 调节时间变长，超调量大

• PID: 引入两个开环零点，一个积分环节

此处可参考 第 3 章 线性系统的时域分析法.md 中对于附加开环零极点影响的总结.

4 广义根轨迹法

闭环传递函数 \(\Phi(s)=\frac{G(s)}{1+G(s)H(s)}\) → 通过整理分母获得根轨迹方程 \(GH= -1\)
如果从一个抽象的数学角度去理解，根轨迹实质上就是一个固定形式的方程 \(K^*D(s) = -1\) , 根据 \(K^*\) 的变化映射出一条曲线.

• 如果\(K^*\)在一般位置，整理成根轨迹要求的标准形式 → 参数根轨迹
• 如果\(K^*\)为负 → 零度根轨迹

4.1 参数根轨迹

根轨迹是根据闭环传函的分母也即特征方程\(D(s)=0\)画出来的.
所以只要 \(D(s)=0\) 相同，闭环传函的极点也就相同. 这就是参数根轨迹中根据 \(G^*(s)\) 的依据.
\(G^*(s)\) 对应的闭环传递函数与原始的闭环传递函数，极点相同，零点不同. 所以只需要用它画根轨迹来获得闭环极点，不要用它分析性质.

用根轨迹法分析二阶系统阻尼比

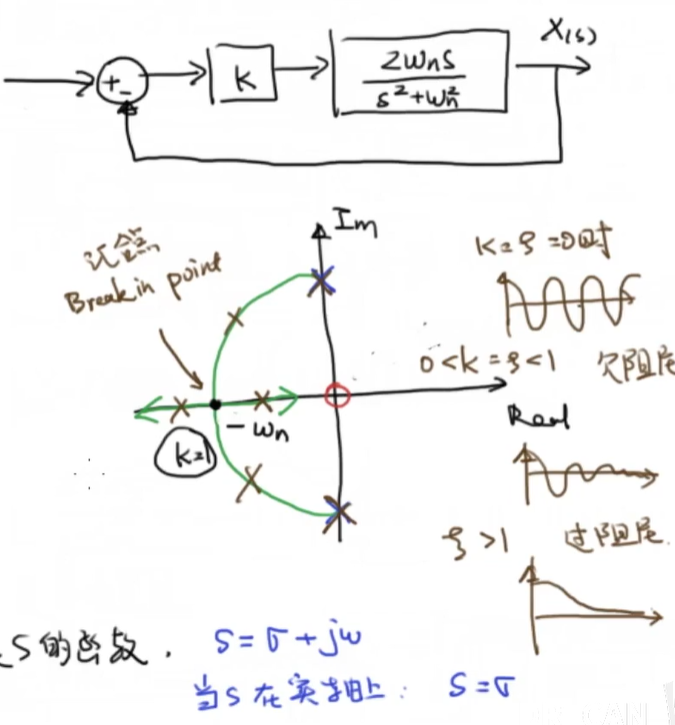
4.2 零度根轨迹

实质上正反馈时的根轨迹

零度根轨迹只是相位变了，画根轨迹时，涉及到\((2k+1)\pi\)的地方都换成\(2k\pi\)即可。

实质上的正反馈

一般我们说的正负反馈只是说在反馈口的符号是正还是负，但是影响正负符号的还有未知参数根轨迹增益！
另外参数根轨迹里面的 \(G^*\) 有可能就变成了零度根轨迹.
根轨迹只关心最终跟轨迹方程是什么样的，如果 \(GH=+ 1\), 就判断实质上是正反馈。

我们一般默认参数都是正的，\(K^*=0\to\infty\), 如果化简发现为 \(GH=1\), 说明系统是正反馈.
另外，就算系统是负反馈，但是如果 \(K^*<0\) 那依旧化简为 \(GH=1\), 实质上是正反馈.

进一步理解：对于负反馈系统

• \(K^*=0\to\infty\), 负反馈，180°根轨迹
• \(K^*=0\to-\infty\), 实质正反馈，0°根轨迹

若令 \(K^*=-\infty\to0\to\infty\), 则两种情况被统一起来，抽象成为一般的数学讨论. 画出包含全部取值的根轨迹.
你会发现零点的选择只是意味着起始点不同，180°根轨迹从起始点往正方向截取，0°根轨迹往负方向截取. 如果你想根据根轨迹确定最佳参数，也许最好正负两段都考虑进去.

截取 0°根轨迹的部分后，箭头方向要取反，因为是往参数减小的方向.

5 上课笔记

---

EXAM NOTIFICATION
英语单词
根轨迹 root locus

一道大题 15 分画根轨迹,
不考出射角入射角，不考初始共轭极点，不考广义根轨迹.
有重极点时需要画多个叉号。

• 求分离点汇合点先求出分离点，然后代入特征方程求 K, 或者使用模为 1 的条件求 K, 如果大于 0 才是分离点.
  • 写出分离点/汇合点的传递函数：根据根轨迹求闭环传递函数: 见笔记相关内容
  • 写出没有超调量 K 的取值范围（根轨迹处于实轴上的部分/不存在共轭极点）画出根轨迹后观察得到实轴上的部分，然后找到 K 小于分离点 K, 大于汇合点 K
• 求与虚轴交点 (与虚轴的交点设为\(j\omega\), 特征方程中 s 换成\(j\omega\), 求出对应的 K 和\(\omega\))
  • 确定稳定时 K 的范围（复半平面左侧部分）, 即 K<与虚轴交点处的 K
    （稳定时 K 的范围求不出可以使用劳斯判据获得结论）

---

根轨迹方程原理：

开环传函\(G_0(s)=G(s)H(s)=\frac{K^*\prod_{j=1}^{m}(s-z_j)}{\prod_{i=1}^{n}(s-p_i)}\)
理想情况下：
根轨迹方程\(1+G(s)H(s)=0\)
即\(1+\frac{K^*\prod_{j=1}^{m}(s-z_j)}{\prod_{i=1}^{n}(s-p_i)}=0\)
\(\Phi(s)=\frac{G(s)}{1+G(s)H(s)}=\frac{G(s)\prod_{i=1}^{n}(s-p_i)}{\prod_{i=1}^{n}(s-p_i)+K^*\prod_{j=1}^{m}(s-z_j)}\)
分子肯定没有零点，是多项式，分子此时都是极点。
这解释了为什么用根轨迹方程算出的 s 就是闭环传函的极点。

同时也能够理解为什么根轨迹（\(K=0\to\infty\)）是从开环传函极点出发，到达开环传函零点（无穷远点）。

当我们要研究的变化的参数 K 不是开环传函的开环增益时，K 在其他位置，就需要化成根轨迹方程的形式。
此时\(1+K^*G_0'(s)\)，其中\(G_0'\)是等效开环传递函数。
化成这种统一的形式，我们才可以用统一的规则来画根轨迹图。

---

根轨迹的基本特性/规则：

为什么根轨迹对称于实轴？
因为极点要么是实数要么是复数，复数一定是共轭的.
为什么复数一定是共轭的，因为出现复数是因为\(as^2+bs+c=0\)的\(\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)会产生共轭根.
三次的一定可以化成\((s-\varphi)(as^2+bs+c)\)其中\(\varphi\)不可能是复数，因为如果是复数的话，s 的系数就会出现复数（似乎这里要设定我们的 s 多项式的系数一定是实数）.
更高次项同理。

拉普拉斯变换和 z 变换的零极点问题
x(t) 或 x[n] 是实信号，其零极点就关于实轴对称，确切说是共轭零极点

为什么开环传递函数极点数 n 大于零点数 m？
如何绘制零点数多于极点数的根轨迹 - 知乎

零点数对应系统输出部分的阶数，在微分方程中对应于输出那部分求导的最高次数。导数项意味着变化趋势（例如加速度对于速度）。如果输出的阶数更高，整个方程就可以理解为未来输出的变化对当前输入有影响，但显然输出必须在输入之后才能产生。所以才说零点多于极点是违背因果律的。
零点大于极点是非因果系统，实际上不存在。
书上似乎有证明？

根轨迹绘制法则，详见 PPT

---

n 阶无差系统的相关题型：
n 阶无差系统是，输入信号最高到 n 阶时，可以保证稳态误差为 0.
严格依照求稳态误差的那个公式，要保证其趋向于 0，说明分子阶数得比分子高！因此，需要让相关参数为 0，才能取掉不应该出现的分子的低阶项/分母的高阶项。

输入信号\(\frac{1}{s},\frac{1}{s^2},\frac{1}{s^3}\)
\(1(t),t,t^2/2\)

---

相角条件是确定 s 平面根轨迹的充要条件

---

根轨迹法的应用：

• 通过轨迹可以判断何时系统稳定：求根轨迹与虚轴交点以及对应的开环增益 K
• 系统何时欠阻尼（根轨迹处于二三象限），系统何时临界阻尼（极点位于分离/汇合点）
• 极点离虚轴越近，稳定性越差。

  参考时域分析法中，振荡环节极点位置，阻尼越小，越靠近虚轴，阻尼为 0 时，极点在虚轴上，阻尼小于 0 时，极点在虚轴右侧.
  第 3 章提到过增加极点，阻尼增大，越靠近虚轴，作用越明显
  有兴趣可以进一步研究.

• 对于单位负反馈系统，闭环零点就是开环零点，闭环极点由根轨迹表示（根轨迹是由开环传函求的，但是求出来的是特征方程的根，是闭环极点）. 闭环 K 就是开环 K
  \(\frac{G}{1+G}=\frac{\frac{KN}{D}}{1+\frac{KN}{D}}=\frac{KN}{D+KN}\)

通过根轨迹确定（指定位置的）开环增益, 对于稳定系统，开环增益与稳态误差有简单的倒数关系.

---

给定要求的阻尼比\(\xi\), 寻找符合要求的开环增益：
\(cos\beta=\xi\), 找到交点即对应的极点.
极点满足\(s=-\xi\omega_n+j\omega_n\sqrt{1-\xi^2}\), 其中有\(\omega_n\)未知.
通过交点处极点满足的相角条件列公式可以获得 s 的准确数值.（那道题刚好有一个极点/零点为(0,0))
通过幅值条件可以获得对应的 K（其实就是代入特征方程求 K 值）

---

求根轨迹思路以及步骤简要总结：

根据我做了几道题以及看了作业题答案后的个人偏好.

根轨迹可以求的其实只有三个：

1. 起始点/（极少情况有起始渐近线）, 出射角
2. 终止点/终止渐近线，入射角
3. 分离点，分离角

当然还有其他的，比如可以确定实轴上的根轨迹，右侧为奇数个零极点的部分是根轨迹.
不过我在做题的时候只是把这个当做验证手段，因为计算了出射角入射角，大致形状以及确定了.

因此做题的时候可以依照这个顺序分别进行计算。

在找渐近线时，如果\(n-m=1\)就不用列式求与实轴交点了.

在计算出射角和入射角的时候，可以统一采用\(\sum^i\angle(s-z_i)-\sum^j\angle(s-p_j)=(2k+1)\pi\)计算（理解了原理后很好记）.
假如说算极点\(p_i\)处的出射点，就把\(\angle(s-p_i)\)换成\(\theta_{p_i}\), 其他地方，将 s 换成\(p_i\). 因为这就是一个逼近. 求得的\(\theta\)是\(p_i\to s\), 刚好就是起始角度.
需要注意的是，求入射角时，同样的方法求出的\(\theta\)是\(z_i\to s\), 但是我们需要的入射角是\(s\to z_i\), 因此需要将求得的\(\theta\)取相反数.

另外在计算\(\angle x+jy\)时，有一个需要注意的地方，就是不可以直接使用\(\arctan{\frac{y}{x}}\)
因为\(\arctan\)适用于实际角度为锐角，当实际角度\(\theta>90^\circ \,or\, \theta<-90^\circ\)时，计算出来的就不对了. 因此需要通过一定的转化.
比如说：\(\angle-1+j\sqrt2\)是一个钝角.
计算时采用\(180^\circ-\arctan\frac{\sqrt{2}}{1}\)（注意这里分母是 1, 不是-1 噢）

还有在画根轨迹的时候需要积累一定的经验，比如说有的时候轨迹就是绕零点的圆，而不是其他形状.

在计算分离点的时候，需要对计算出来的结果进行判断（此时 K 是否大于 0/是否在 K>0 画出来的根轨迹上，才符合条件）.
除特殊情况外，分离点是实数，可以直接通过判断分离点是否在实轴根轨迹上确定. 因为右侧零极点个数为奇数的才是根轨迹.
特殊情况下比如说下图，这种情况下通过根轨迹一画就知道，因为两个根轨迹直线相向而行，必定会在某处相交，其他情况基本可以判断舍去（吧）.

alt

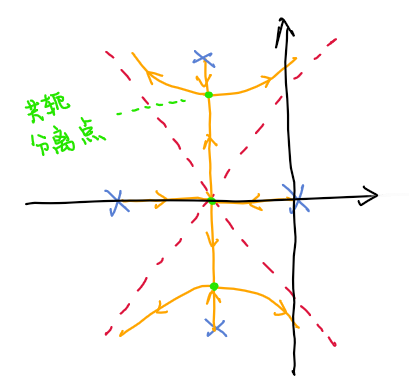
考试不会对分离点考察太难，三阶的话一般可以猜到一个通过长除法化成二阶，再高就只能编程计算了.

---

闭环零极点分布对系统的影响

• 对时间响应/阶跃响应
  • 主导极点决定系统主要的动态特性
  • 闭环偶极子互相抵消

如果\(m\neq n\), 就会存在渐近线，参考\(\theta=\frac{(2k+1)\pi}{n-m}\)

增加开环零极点	\(n---m\)	\(\theta\)	稳定性	解释
增加极点	↑	↓	不利	渐近线右偏，到达正半平面
增加零点	↓	↑	有利	渐近线左偏

K>0 时系统稳定，称为结构稳定（根轨迹全部在左半平面）

ATTENTION: 增加零极点一般都是默认增加 S 左半平面的.
增加开环右零点，根据奈氏判据，是会破坏稳定性的.
增加开环右极点，也会导致根轨迹有一部分在右半平面.

---

考试不考广义根轨迹，不考出射角/入射角（因为根轨迹频率会考）