Skip to content

CH4. 线性系统综合

1 状态反馈与输出反馈

  • 状态反馈 \(u=w-KX\)
  • 输出反馈 \(u=w-HY\)

两种反馈都可以改变极点，阶数不变，A 变了，但是输出反馈能做到的，状态反馈也能做到 (\(K=HC\)), 反之则不亦然. 状态反馈可以任意配置（可控的）极点. （系统不完全能控时，只能任意配置可控的 r 个极点）

状态反馈有可能改变系统的能观性。

反馈类型 能控性 能观性
状态反馈 不变 可能变（零极点相消）
输出反馈 不变 不变

2 极点配置控制器

状态空间中系统的镇定问题，即让系统渐近稳定

\(\sum(A,B,C)\leftrightarrow \sum(A-BK,B,C)\) , \(A-BK\) 极点都在 s 左半平面

2.1 能控性与极点配置

  • 系统完全能控，则状态反馈能镇定，极点可以任意配置
  • 系统不完全能控，则当不可控极点位于左半平面时，状态反馈能镇定.
    不可控极点不能被修改，其余极点可以被修改.

2.2 K 的计算

  • 根据时域/频域性能指标，用经典控制理论确定期望极点位置，然后就确定了期望的特征方程，进而就确定了对应的 K
  • LQR 控制器，最优化代价函数的方法

对于第一种方法，步骤如下：

  1. 判断完全能控
  2. 化成能控标准型 \(X=T\hat X\)
  3. 根据能控标准型写出特征多项式 (A 最后一行）
  4. 根据期望极点写出期望特征多项式
  5. \(\hat K=p^*-p\)

  6. \(K=\hat KT^{-1}\)

    对原系统：\(u=w-KX\)
    经过坐标变换后，\(u=w-KT\hat X\)
    说明 \(\hat K=KT\).

当然，如果系统阶次比较低，根据特征多项式不变的特性（化成标准型也只是为了方便看出特征多项式的系数）, 可以直接 \(|sI-(A-BK)|=\text{期望特征多项式}\) , 对应系数相等求出 \(k_i\)

对于不完全能控的系统，可以根据能控性分解，对能控部分（前 r 行）控制；也可以使用待定系数法计算低阶系统的 K（后面有总结）

3 状态观测器

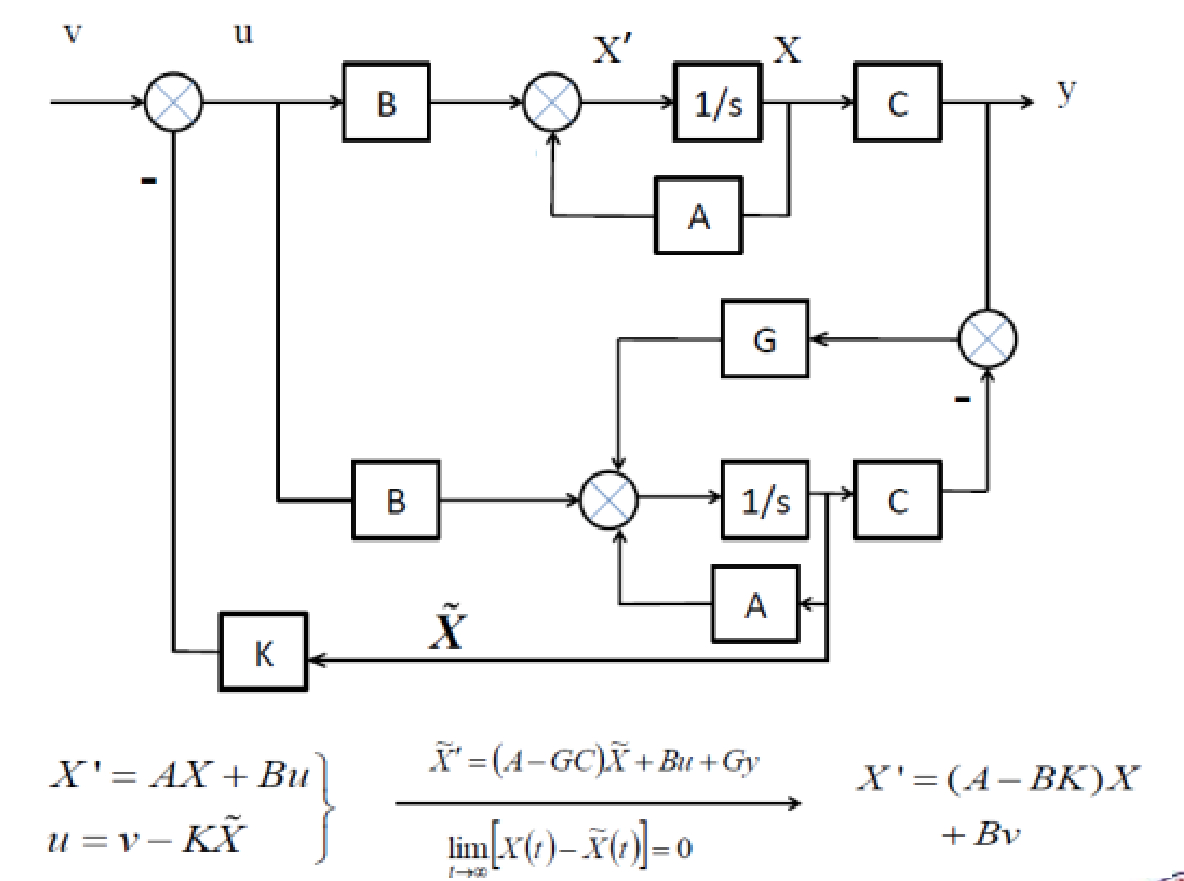
符号表达有的是 L, 有的是 G

龙伯格观测器

整理可得 \(\dot e=\dot X-\dot {\hat X}=(A-LC)(X-\hat X)\).

建立观测器，实际上是建立一个新的反馈系统，当\(A-LC\) 特征值具有负实部时，误差\(e\)趋于 0

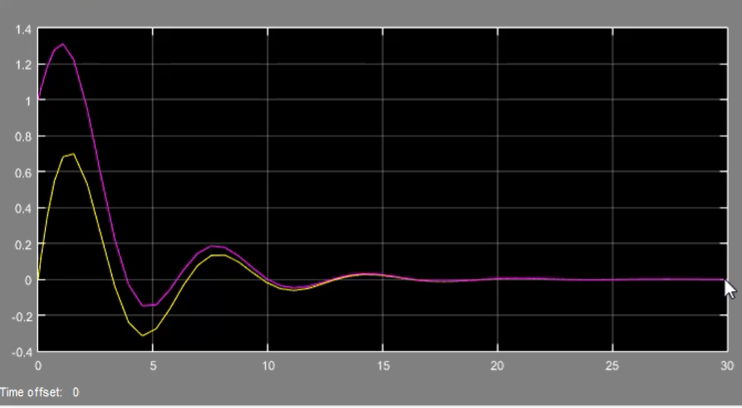
3.1 设计步骤

系统完全能观，或者不能观部分渐近稳定，才能设计观测器.

  1. 全维观测器 \(\dot {\hat X}=(A+MC)\hat X+Bu-My\) 通过配置 M, 使这个观测器渐近稳定，则 \(\lim_{t\to\infty}(x(t)-\hat x(t))=0\)

    1. 判别能观性
    2. 化成能观标准型，可以读出特征方程系数
    3. 期望的观测器极点⇒ 期望特征方程系数
    4. 观测器 \(\hat M\)
    5. 原系统 \(M=T\hat M\)

    6. 观测器方程

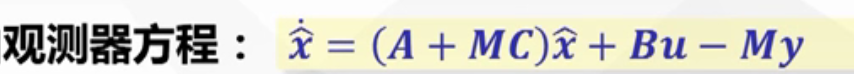
  2. 降维观测器：这个没掌握 QWQ

3.2 其他

使用全维观测器的方法观测常值扰动

4 极点配置与状态观测器配置总结

两者都是通过对 A 进行线性变换，从而进行极点配置. （配置 A 的特征根/特征值）
只不过极点配置是配置原系统的极点，状态观测器配置是配置观测器极点（要求响应更快）


如果已知的状态方程是标准型，那么就可以大大简化步骤，可见之前讲能控能观标准型及其互相转化的意义.

第二个方法具体解释

原始思路比较绕：一个普通系统 → 转化为标准型 → 极点配置得到标准型的控制器 \(\tilde{K}\) → 还原为原系统的控制器 \(K\)
图片笔记里提到的方法是改进过的，就是出于计算简化的目的省去了化标准型这一步，因为这一步的目的在于取得原系统特征方程的系数. 而这个系数可以由计算行列式 \(|sI-A|\) 得到.

5 带状态观测器的（状态反馈）闭环控制系统

5.1 分离原理/分离特性 Seperation Principal

已知观测器

\[ \begin{aligned} \dot{\hat X}&=A\hat X+Bu+L(y-\hat y)\\ \dot {e}&=X-\hat X=(A-LC)e \end{aligned} \]

又有控制律\(u=-K\hat X\), 则有

\[ \dot X=AX-Bu=(A-BK)X+BKe \]

把两部分系统合起来（具体来说就是状态 X 和状态 e 合起来）, 则有带权威状态观测器的闭环控制系统的状态空间模型：

\[ \begin{aligned} \begin{bmatrix}\dot X\\\dot e\end{bmatrix}&= \begin{bmatrix}A-BK & BK\\0&A-LC\end{bmatrix} \begin{bmatrix}X\\e\end{bmatrix}\\ y&= \begin{bmatrix}C&0\end{bmatrix} \begin{bmatrix}X&e\end{bmatrix} \end{aligned} \]
  • A-BK, A-GC 共同组成了整个闭环系统的特征值
  • 极点配置控制器和观测器可以分别设计

  • 为了保证良好的控指标，观测器极点的实部要远小于原系统配置极点的实部

5.2 传递函数的不变性

添加观测器后，闭环传递函数不变. （毕竟观测器部分是不能控部分，不反应在传函上）

6 LQR 控制器

极点配置的时候，如何决定目标特征值？这里通过 cost Function 求解.

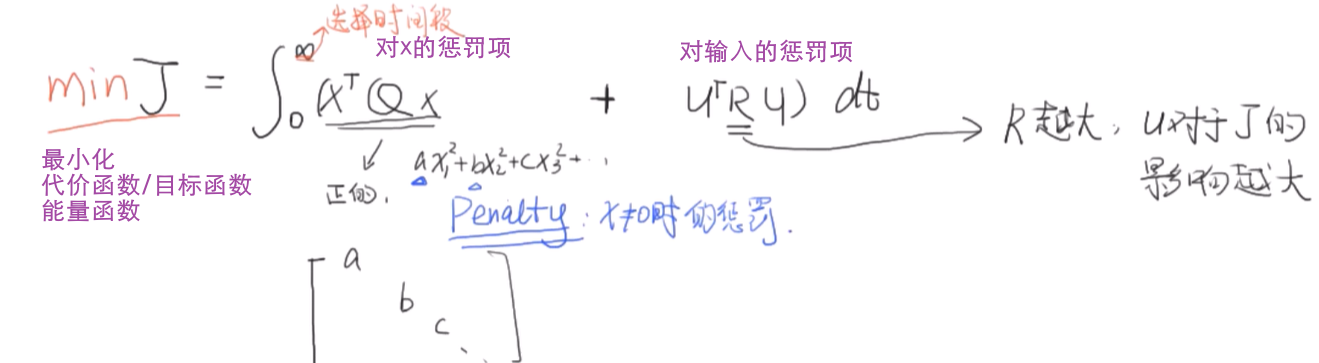
Q 比较大时，系统倾向于快速稳定，R 比较大时，系统倾向于减小能耗.

LQR 设计步骤：

  1. 选取合适的 Q 和 R

  2. 解 Riccati 方程计算出 K

    MATLAB K=lqr(A, B, Q, R) 可以计算得到极点配置的 K

6.1 轨迹跟踪

【Advanced 控制理论】8.5_线性控制器设计_轨迹跟踪 (Follow a Desired Path)_哔哩哔哩_bilibili

看了一下大概思路是：期望值是\(x_d\) （可以是\(x_d(t)\) ), 令\(e=x_d-x\) 作为”状态变量”, 到达稳态其趋于 0,x 就趋于\(x_d\).

实际上结果就是输入添加了一个常数。

Back to top