Skip to content

第二章 控制系统的数学模型

1 列微分方程

电感 \(u=L\frac{di}{dt}\) ⇒ \(\frac{U}{I}=sL\)

电容 \(i=C\frac{du}{dt}\)⇒ \(\frac{U}{I}=\frac{1}{sC}\)

此外，阻尼 好像是一个挺常见的概念，但是没学过. 我觉得可以理解成一个和速度成正比的阻力.

  • 虎克定律：弹力 \(f=kx\)
  • 粘性摩擦定律：粘性摩擦力 \(f=k\dot x\)

2 拉氏变换获得传递函数

（完整版） 拉氏变换常用公式 - 百度文库
常用拉氏变换表

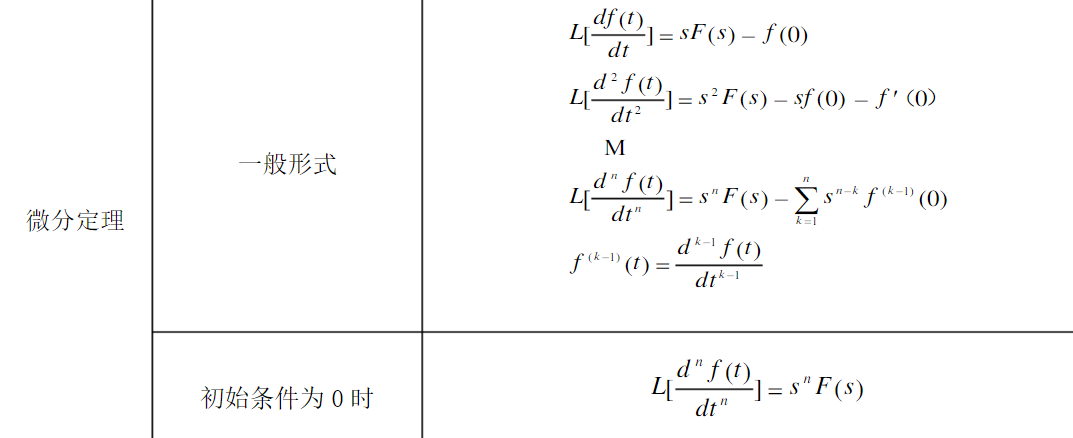
  • 实位移 \(f(t-\tau)\to e^{-\tau s}F(s)\)
  • 复位移 \(e^{-at}f(t)\to F(s+a)\)
  • 终值定理
    使用终值定理的条件是：系统的极点都在复平面的左边 （首先要有终值，求出的终值才是有意义的，否则好像是平均值？）

2.1 一个问题

系统的单位阶跃响应为：\(y(t)=1-e^{-2t}+2te^{-2t}\)
则系统的单位脉冲响应为：\(y(t)=4e^{-2t}-4te^{-2t}\)
而非：\(y(t)=\delta(t)+4e^{-2t}-4te^{-2t}\)

为什么 1 求导是 0 而不是\(\delta(t)\), 我觉得可以这样理解：

  • 这里的 1 是全实域的常数 1, 只不过一般我们只关心 \(t>0\) 的时刻
  • 如果 1 是阶跃，会标明 \(\varepsilon(t)\)
  • \(G(s)\) 分母阶数等于分子阶数时，才会出现输出有阶跃/冲击 （吧）

自控里只关心 \(t>0\) 的信号，拉氏变换采用的是 "单边拉氏变换" \(F(s)=\int_0^{\infty}f(t)e^{-st}dt\)
所以这是一个比较 tricky 的点，我们总说阶跃信号的拉氏变换为 \(\frac{1}{s}\)
但是对于常数 1, 拉氏变换也会得到 \(\frac{1}{s}\)
所以 \(\frac{1}{s}\) 反变换得到的 1, 是阶跃还是常数 1?
可能这是为什么会有开头那个问题。

3 控制理论的一些基本概念

传递函数\(\Phi(s)\)的增益或者传递系数, 即放大信号的倍数，假设输入信号是一个常值（阶跃信号\(\frac1s\)), 根据中值定理，\(\lim_{s\to0}s\frac1s\Phi(s)=\lim_{s\to0}\Phi(s)\)

因此我们把传递函数里的 s 都置零后得到的常数就称为增益. （对于分母有 \(s^v\) 的，忽略掉这部分）

开环传递函数的是开环增益, 闭环传递函数的是闭环增益. 一般我们把传递函数写成尾一式、归一式，那么分子的 K 就是增益值.

另外还有一个概念，专门针对开环传递函数写成首一式时的 K, 称为根轨迹增益.

4 上课笔记

EXAM NOTIFICATION
考试不考结构图化简
梅森增益公式一道大题 10 分，信号流图/结构图直接写梅森增益公式.（详见笔记相关内容.)

三种传递函数的形式（求开环增益：去掉积分环节，s 趋向 0 时的常数）

  • 一般式
  • 零极点式/首一式：根轨迹增益
  • 时间常数式：频率特性，增益

微分方程与传递函数互相推导.
(n 阶微分就是 sn, 唯一需要注意的可能就是初始值不为零时，由微分方程求传递函数，最下面有微分定理\(sF(s)-f(0)\))

英语单词
零点 zero
极点 pole
特征根 characteristic root
特征方程 characteristic equation
传递函数 transfer function
频率特性 frequency characteristic

系统建模的方法

  • 解析法：了解系统的原理，列出微分方程
  • 实验法：施加测试信号，利用数学模型逼近

要注意传递函数的负载效应问题。要在系统正常工作的情况下建立系统模型。

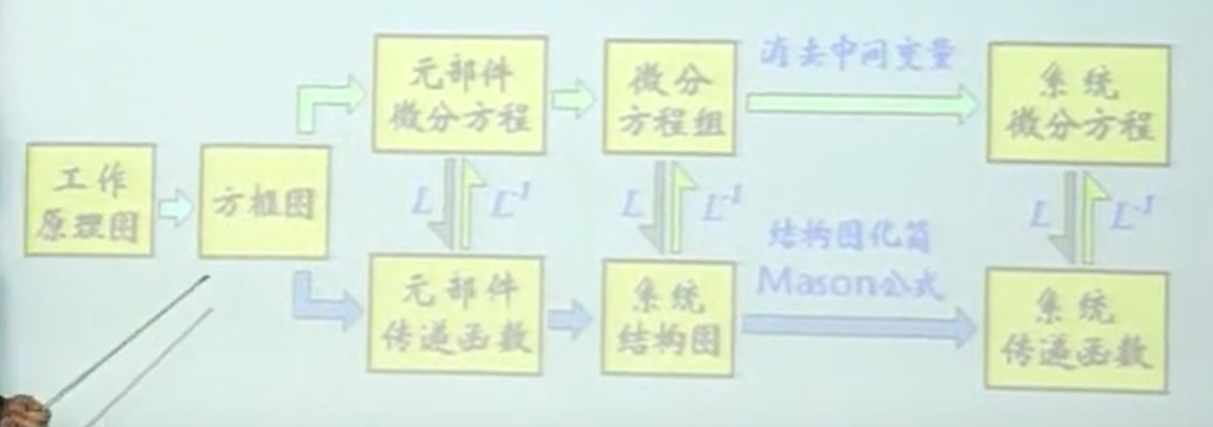
图片想说明的意思是，我们可以先画出系统的原理图/工作框图，弄清楚各个部分之间的关系.
然后有两条路径，第一条是列元件的微分方程组，求解之后拉氏变换为传递函数.
第二条是根据元部件传递函数，列出系统框图，根据梅森增益公式求出系统传递函数（显然应该使用这种方法）

数学模型的类别：

  • 时域：
    • 微分方程
    • 差分方程
    • 状态方程
  • 复数域
    • 传递函数
    • 结构图
  • 频域
    • 频率特性

传递函数

  • 复变量 s 的有理真分式函数，\(m\le n\), 分母阶数不大于分子阶数，且所有系数均为实数.
  • 只取决于系统本身的结构与参数，与输入量无关.
  • 可以与微分方程互相转化。零初始条件下，只需要微分方程的算符\(\frac{d}{dt}\)与 s 转换，就可以了.
  • 反变换是冲激响应

传递函数的局限性：
只能表示线性定常系统
适合描述单输入单输出
原则上不反映非零初始条件时系统响应的全部信息

注意，后面讲的所有内容都有一个前提：系统是线性定常系统。
微分方程的形式需要满足：

  1. 每一项都是输入/输出的本身或者 n 阶导数（一阶），没有（不同阶数的）交叉乘积项，没有（同一阶数的）平方（二阶）等高次项，也没有常数（零阶）。
  2. 每一项的系数恒定

世界上没有线性系统，只有泰勒级数一阶展开。

非线性微分方程的线性化：切线法/小偏差法
（泰勒级数一阶展开，泰勒级数展开略去 2 阶及以上）
$$
f(x)-f(x_0)=(\frac{df(x)}{dx})_{x_0}(x-x_0)
$$
即线性化方程为\(y=(\frac{df(x)}{dx})_{x_0}x\).

运动的模态/线性微分方程解的类型
线性微分方程的解=特解（输入决定）+通解（系统本身决定）
通解形式：每个微分方程特征根对应一种模态/振型，通解是所有特征根对应模态的和。

  • 实数单根 \(e^{\lambda_i t}\)
  • 实数重根 \(t^{n}e^{\lambda_i t}\)
  • 共轭复根 \(e^{(\sigma+j\omega) t}=e^{\sigma t}(\cos(\omega t)+\sin(\omega t))\)

从拉普拉斯变换式/传递函数的角度理解（零极点）：

\[H(s)=\frac{C_1}{s-\lambda_1}+\frac{C_2}{s-\lambda_2}+...+\frac{C_n}{s-\lambda_n}\]
  • 极点，特征根：\(\lambda_i\)
  • 模态，振型：\(e^{\lambda_it}\)

极点决定了组成输出的信号的基本类型（指数衰减，三角函数等）
零点影响了每种模态的系数\(a_k\)，零点越接近虚轴，对应分量系数越大。具体原因似乎是是留数法过程中的一些影响，但是留数法怎么求我忘了，以后有时间可以分析一下。

开环传递函数_百度百科
闭环传递函数_百度百科

  • 开环传递函数：
    • 开环传递函数是指一个开环系统（没有反馈的系统）的输出与输入之比与频率的函数关系，即系统的频率域特性。
    • 也可以指一个闭环系统的反馈量输出与输入之比与频率的函数关系。\(G(s)H(s)\)（似乎使用\(G_0\)表示）
  • 闭环传递函数：在负反馈闭环系统中，假设系统单输入 R(s); 单输出 C(s), 前向通道传递函数 G(s), 反馈为负反馈 H(s)。此闭环系统的闭环传递函数为 \(\frac{G(s)}{1+G(s)H(s)}\)，可以表示为\(\Phi(s)\)。

小结论：对于单位负反馈

\[ H(s)=\frac{G(s)}{1+G(s)}=\frac{\frac{a}{b}}{1+\frac{a}{b}}=\frac{a}{a+b}=\frac{1}{\frac{1}{G(s)}+1} \]

根据所需要的形式快速获得结果。

系统传递结构（？）表达方式：

  • 控制系统的（典型）结构图
    • 有向线条代表信号
    • 方框代表传递函数
    • 求和点（圆圈里面是叉号）
  • 信号流图
    • 小圆圈代表信号
    • 有向线条代表传递函数
    • 利用传递函数正负代表求和

如果从结构图画信号流图，一个比较稳的方法是：把系统结构图中的框都变成线，把线都变成圈。
然后支路增益为 1 的相邻两个节点可以合并成一个节点（除了源节点和输出节点）

为什么要画信号流图？因为通过信号流图可以列写出梅森增益公式，可以方便地获取到某一个输入与某一个输出之间的传递函数。
但其实也可以直接从典型结构图直接列写梅森增益公式。

  • 通过典型结构图求传递函数
    • 先化简，然后照着回路列输入输出关系，消除中间变量（化简太麻烦，不推荐！可以参考课本例题2-18，不过我感觉有一个好处就是，结构图不是很复杂的话，照着信号传递列式子，可以直接获得多输入输出的关系式）√
    • 列梅森增益公式√√√
  • 通过信号流图求传递函数
    • 列梅森增益公式√√

总而言之，言而总之，这部分知识点主要是通过结构图/信号流图列出输入输出关系就可以了！（简化系统函数的计算）

另外梅森增益公式求的是某一个输入与某一个输出之间的关系（换言之也是求出了指定输入的输出），如果想要求输入R(s)与扰动N(s)共同作用的输出，则采用叠加定理，将彼此分别置零后，求出的两个输出叠加在一起。

感觉这样的过程挺不错的

过程举例

考试方法总结！
求梅森增益公式（包括根据结构图直接写）的方法归纳：

一个遍历方法：define F(node,condition):
从一个点 node 出发，遇到分叉就分叉，走到终点（满足 condition, 不能再继续走下去，可能是满足了所需要求，可能是不符合梅森增益公式中路径要求不重复走走过的结点的要求）就结束 return，最终遍历出所有路径.
称之为方法 F(node,condition)

  1. 求 L
  2. 找到每一个有输入的结点（混合结点）node
  3. F(node, 组成一个闭合回路）
  4. 求\(\Delta\)
  5. 求 P: F(node, 到达目标节点）

根据结构图直接写梅森增益公式的一个难点在于，sum 不好处理，其实可以把 sum 当做一个信号/结点
其他地方则是数据线当做一个结点，方框当做一个线

传递系数的定义：（如果G(s)为开环传函）

\[ K_0=\lim_{s\to0}s^rG(s)=K\frac{\prod_{i=1}^m (-z_i)}{\prod_{j=1}^n (-p_j)}=\frac{b_0}{a_0} \]

（上面应该是除去所有的零极点\(p_j\)的连乘）

特殊地，如果如果G(s)为开环传函：
零极点形式的 K，叫做根轨迹增益；
时间常数形式的\(K_0\)，叫做开环比例系数。

求开环增益/开环比例系数时，直接使 s 趋向 0 求极限即可.
求根轨迹增益时，直接使各个乘积项尾部为 1, 提出的系数合在一起就可以了.

题干中给\(c(t)=1-e^{-2t}+e^{-t},r(t)=1(t)\)
求冲激响应\(k(t)\).
有一个想法是，直接对\(c(t)\)求导，似乎就是结果。
有个陷阱是，没有说明初始状态是不是零状态！就比如说对 1 求导，可能是恒值 1（结果为 0），也可能是阶跃信号\(1(t)\)（结果为\(\delta(t)\)），或者其他。
因此，遇到这种问题，一定要使用拉氏变换求解（不受初始状态影响），\(\Phi(s)=\frac{C(s)}{R(s)}\)，然后反变换获得冲激响应。

拉氏变换
\(F(s)=\int_{0}^{\infty}f(t)e^{-ts}dt\)
\(f(t)=\frac{1}{2\pi j}\int_{\sigma-j\infty}^{\sigma+j\infty}F(s)e^{ts}ds\)

常见函数 \(f(t)\) \(F(s)\)
单位脉冲 \(\delta(t)\) \(1\)
单位阶跃 \(1(t)\) \(1/s\)
单位斜坡 \(t\) \(1/s^2\)
单位加速度 \(t^2/2\) \(1/s^3\)
指数函数 \(e^{-at}\) \(1/(s+a)\)
正弦函数 \(\sin\omega t\) \(\omega/(s^2+\omega^2)\)
余弦函数 \(\cos\omega t\) \(s/(s^2+\omega^2)\)

反变换：

  1. 公式法
  2. 查表法/分解部分分式法
  3. 试凑法
  4. 系数比较法
  5. 留数法

留数法之前复变函数证明过，回来有机会再整理吧.
其实挺好理解的。（题目中遇到的似乎都很简单！)
\(C_1=\frac{1}{(m-1)!}\lim_{s\to p_i}\frac{d^{(m-1)}}{ds^{(m-1)}}[(s-p_i)^mF(s)]\)

Back to top