Skip to content

Ch5. 非线性控制理论

来源: DR_CAN 非线性控制理论 bilibili
由于时间关系没有仔细看完, 如果有需要可以再看看

1 Lyapunov 直接方法

部分知识参考系统稳定性部分.

\[ \begin{cases} \dot x_1&=\cdots=f_1\\ \dot x_2&=\cdots=f_2\\ V&=\cdots \end{cases}\Rightarrow \dot V=\nabla V\times f= \begin{bmatrix}\frac{\partial V}{\partial x_1}&\frac{\partial V}{\partial x_2}\end{bmatrix} \begin{bmatrix}f_1\\f_2\end{bmatrix} \]

1.1 单摆模型为例分析稳定性

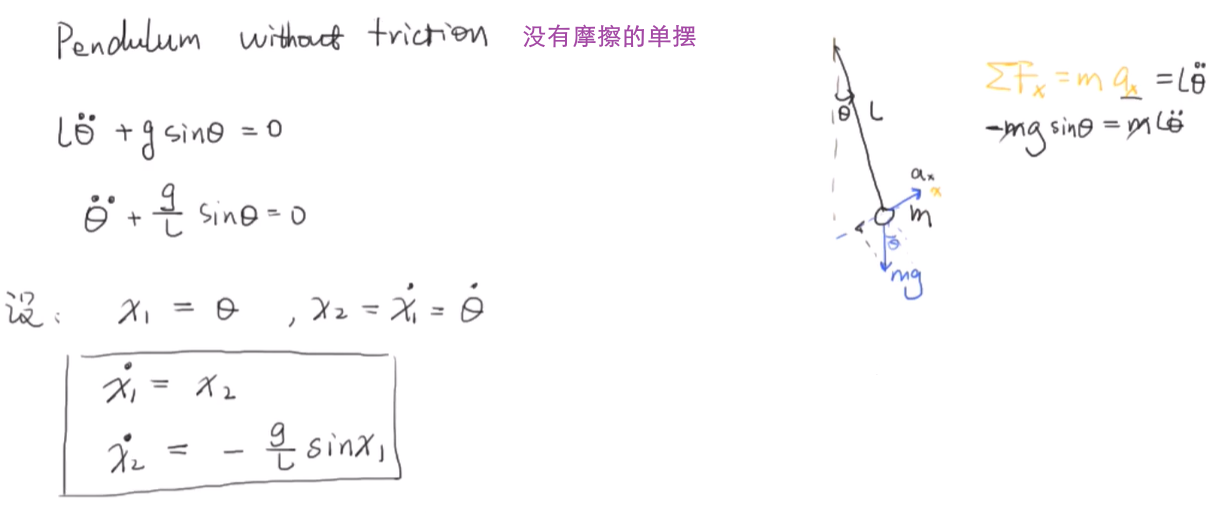
模型搭建: 牛顿第二定律 F=ma

其中 \(F= -mg\sin\theta\), \(a=\ddot{\theta}L\) , 整理能够得到 \(\ddot \theta+\frac{g}{L}\sin\theta=0\).

之后选取状态 \(x_1=\theta,x_2=\dot x_1=\dot\theta\) 搭建状态方程, 如图所示.

构造李雅普诺夫函数时可以从能量入手, 即 动能+势能.

\(V=\frac12mv^2+mgh,\;v=x_2L,\;h=L(1-\cos x_1)\)

考虑摩擦力和速度成正比, \(f=kv=kL\dot\theta\)

1.2 不变性原理

之前提到, \(\dot V\) 负定时, 系统渐进稳定; 半负定时, 系统稳定.

这里扩充一下, 如果 \(\dot V\) 半负定, 但是除了 \(X=0\) 以外 \(\dot V\ne0\), 则系统渐近稳定.

可以令 \(\dot V=0\), 联立前面的所有式子, 看看能不能推出 \(X=0\)

2 Nonlinear Backstepping Controller 反馈线性化控制

非线性系统的基础反馈稳定控制器: 系统结构完全知道的时候, 可以通过控制输入 u, 消除掉对应的非线性项, 或者消除 \(\dot V\) 中非负定的部分.

因为输入 u 的表达式是关于状态 x 的函数(为了消除非线性部分), 所以实际上是反馈控制.

Nonlinear Backstepping Controller (反步设计法):

通过控制 u 为 x 的函数, 使整个系统线性化. (Feedback Linearization)

【Advanced控制理论】15_Nonlinear Backstepping Control_反馈线性化控制_Feedback Linearization_哔哩哔哩_bilibili 有很多公式推导.

从推导中有一个很重要的思想, 就是如果我们希望系统在某一个点稳定下来, 就列一个李雅普诺夫函数V, 然后看一下要使 \(\dot V\)负定需要满足什么条件. 然后接着提出一个目标, 要达到这个目标需要什么... 以此类推, 最终得到一个 u 关于 x 的函数.

【Advanced控制理论】15.5_Nonlinear Backstepping Controller_补充习题_(未剪辑视频)_哔哩哔哩_bilibili

3 Nonlinear Adaptive Controller 自适应控制器

思想和上面那个差不多, 需要知道系统结构, 但是这里假设某个参数是缓慢变化的”未知常数”.

4 非线性鲁棒控制

4.1 滑模控制

除了控制输入，其他都当作扰动，通过ESO消除，ADRC

Back to top