Skip to content

CH1. 系统的状态空间模型

1 状态和状态空间模型

线性系统状态空间模型可由积分器、加法器、比例器组成

本页之后用到的一些概念总结

友矩阵：大概长这个样子，\(\begin{bmatrix}0 & & I\\ -a_n & \cdots & -a_1\end{bmatrix}\), 最后一行可以直接写出该矩阵特征多项式.
对角矩阵：略
约当标准型：有的矩阵不能相似对角化，但是可以化为约当型

能控标准型：A 为友矩阵，B 最后一行为 1
能观标准型：A 为友矩阵，C 最后一列为 1

2 建立状态空间模型

机理建模：根据系统的物理机理建立对象的数学模型

  • 弹簧 \(F=kx\)
  • 阻尼 \(F=k\dot x=kv\)
graph LR
  A["微分方程（组）"] -->|1, 3| B[状态空间方程];
  A --> |2| C["传递函数（阵）"];
  C --> |4| B;

  1. 机理建模: 通过物理机理列写微分方程组后，选取合适的状态变量（一般选择储能信号，例如电容电压）, 之后整理成\(\dot {x_1}=f(\cdots)\)的格式，最后写成状态方程形式
    ✨这种方法获得的状态变量比较直观，可以单独列每个元件的数学表达式，不用整理成 3 那样的微分方程
    不过状态空间方程不是任何一类标准的形式.

  2. 对于 SISO 的单微分方程，拉氏变换之后即可整理成传递函数

  3. 由高阶常微分方程建立状态空间模型：\(y^{(n)}+a_1y^{(n-1)}+\cdots+a_ny=b_0u^{(n)}+\cdots+b_nu\)

    1. 微分方程中不含输入量的导数项
    2. 微分方程中含包含输入量的导数项

    ✨此方法获得的 A 为友矩阵，B 最后一行为 b, C 第一列为 1. 不是能控/能观标准型
    但是此方法获得的系统一定是能控的！

  4. 传递函数的实现: 见 这里

输入含导数项的状态空间方程的小总结

  1. 把方程列成标准形式，注意缺少的项要补齐，比如说右侧输入项与输出项同阶次的.
  2. 标好 a,b 都是什么.
  3. n 阶方程，状态方程也是 n 阶的（可以先画出状态方程的大致形状）
  4. 先求\(\beta_0\sim\beta_n\)
  5. 再求\(x_1\sim x_{n+1}\) 其中 \(x_{n+1}\) 只是占个位，不是状态变量
  6. 再写出\(\dot x_1\sim \dot x_{n}\) 其中 由于不知道 \(x_{n+1}\), \(\dot x_{n}\)通过记额外的公式写出来.
  7. 得出结果

不同形态状态空间方程之间的互相转换

这个太多了。. 就不总结了...
可以看约当标准型部分：其他形式变约当标准型. 把状态空间方程化成约当标准型
传递函数的实现问题

3 线性定常系统状态方程的解

求输出的方法总结

3.1 状态转移矩阵

  1. \(\phi(0)=I\) 时间不变，状态不转移（选取的状态不能突变）

  2. 组合性质 \(\phi(t_2)=\phi(t_2-t_1)\phi(t_1)\)
    \(X(t_2)=\phi(t_2-t_1)\phi(t_1)X(0)\)

  3. \([\phi(t)]^{-1}=\phi(-t)\)

求状态转移矩阵的方法

  1. 直接展开级数（不推荐，拟合太难

  2. 如果是对角标准型，则对角线上的 \(\lambda\) 变成 \(e^{\lambda t}\)
    如果是约当标准型，则....
    可以把 A 变换为上述标准型

  3. 拉氏变换法 \(L^{-1}\{(sI-A)^{-1}\}\)

  4. 凯莱-哈密顿定理（这个我不会~）

3.2 齐次解 \(\dot X=AX\)

\(X(t)=e^{At}X_0\)

  1. \(e^{At}\) 可以幂级数展开 （不推荐）
  2. 拉氏变换求解 \(L^{-1}\{(sI-A)^{-1}\}\)

渐近稳定，A 的特征值均具有负实部

3.3 非齐次解

  1. 时域求卷积\(x(t)=\int_0^te^{A\tau}u(t-\tau)d\tau=\int_0^te^{A(t-\tau)}u(\tau)d\tau\). （注意这个形式比较灵活，卷积位置可交换）
  2. 拉氏变换 \(X(s)=(sI-A)^{-1}[X_0+BU(s)]\).

其实有时候第一个方法比较简单。
比如说输入为阶跃信号，那么 \(x(t)=\int_0^te^{A\tau}u(t-\tau)d\tau=\int_0^te^{A\tau}d\tau\) , 只需要进行积分即可. 拉氏变换需要分解因式再反变换.

还比如说输入是一个分段函数，第二个方法可能就会非常复杂，第一个只需要分段求积分.

4 相图 ⇋ 特征值 ⇋ 稳定性

【Advanced 控制理论】3_Phase Portrait_相图_相轨迹_哔哩哔哩_bilibili

相图，似乎当初经典控制理论课程中讲过，这里就不赘述了..

对于下图简单的情形：只有 2 个状态，且微分方程简单如下，通过分类讨论能够得出可能的情况.

source: 源；saddle: 鞍；sink: to fall or drop to a lower place or level

当且仅当 a, d 都小于 0 的时候，系统才是稳定的，\(t\to\infty\) 时，\(x_1,x_2\to0\)

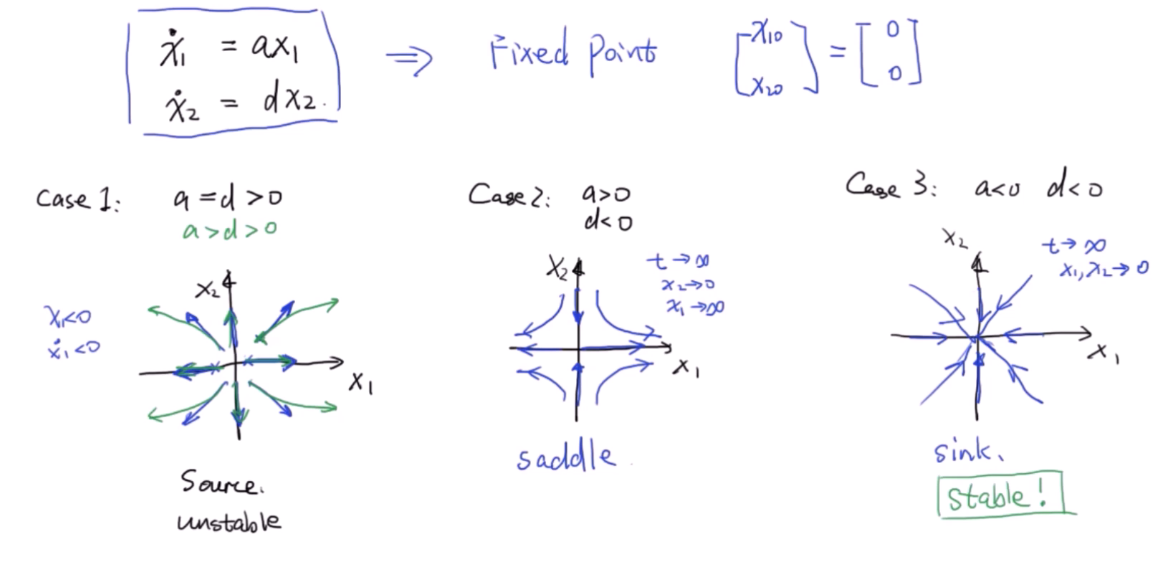
通过线性变换\(P^{-1}AP=\Lambda\), 能够把一般的状态空间\(\dot X=AX\)变换成上述的简单情况\(\dot Y=\Lambda Y\). 因此易得，原状态空间的相轨迹也是由 a, d 决定的. 而 a, d 其实就是状态矩阵 A 的特征值. AKA, 特征值决定系统稳定性.

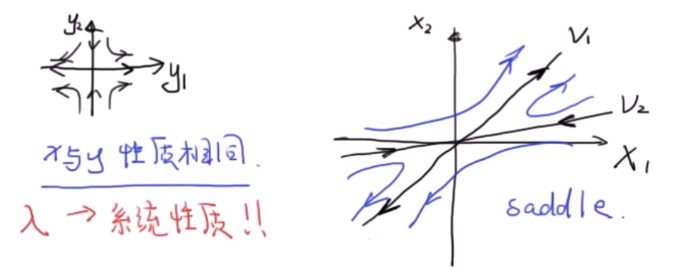
对于更复杂的系统，相轨迹也更加复杂，这里就不记录了，可以见原视频. 总之都由系统的特征值有关.

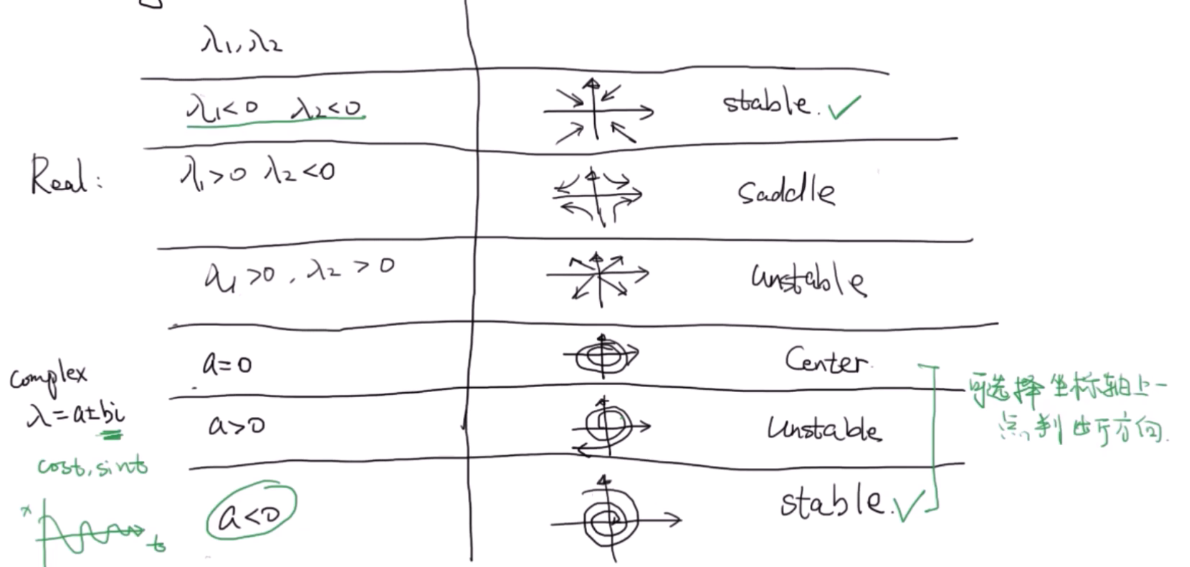
关于状态矩阵特征值和传递函数极点，可以用下面这俩理解

  • 求特征值 \(|\lambda I-A|\).
  • 求传递函数 \(C(sI-A)^{-1}B=C\frac{adj (sI-A)}{|sI-A|}B\)

5 系统线性变换、等价变换、状态变换 \(X=T\hat X\)

\(\hat A=T^{-1}AT\), \(\hat B=T^{-1}B\), \(\hat C=CT\)

  1. 代数上等价，输入输出特性不变
  2. 特征值不变，特征多项式系数不变，极点不变
  3. 传递函数阵不变
  4. 能控性能观性不变

线性定常系统特征值对线性变换具有不变性，因此线性变换 (\(T\)可逆的变换）是等价变换
上述性质默认前提为线性系统（非线性系统不知道）

广义特征向量

限于时间精力，这里就不详细解释了..

把状态空间方程化成约当标准型：

  1. 特征值都不同⇒对角标准型 （参考线性代数相似对角化，对角线上是特征值）
  2. 特征值有重根⇒约当标准型 （广义特征向量）

状态空间方程化成约当标准型

友矩阵

大概长这个样子，\(\begin{bmatrix}0 & & I\\ -a_n & \cdots & -a_1\end{bmatrix}\)

很多标准形式的状态矩阵都是友矩阵。

能控标准型化为约当标准型：
友矩阵特征值互异时，将友矩阵变换成对角线阵的变换矩阵恰为范德蒙矩阵.

\[ \Lambda=\tilde{A}=P^{-1}AP= \begin{bmatrix} 1 & 1 & 1 \\ \lambda_1 & \lambda_2 & \lambda_3 \\ \lambda_1^2 & \lambda_2^2 & \lambda_3^2 \\ \end{bmatrix}^{-1} \begin{bmatrix} 0 & & I\\ -a_n & \cdots & -a_1 \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \\ \lambda_1 & \lambda_2 & \lambda_3 \\ \lambda_1^2 & \lambda_2^2 & \lambda_3^2 \\ \end{bmatrix} \]

作用：\(\phi(t)=e^{At}=e^{P\tilde{A}P^{-1}t}=Pe^{\tilde{A}t}P^{-1}\)
其中\(e^{\tilde{A}t}\)可以直接写出来（对角线取指数）, \(P\)也可以由特征值直接写出来.
有些情况下，可以简化求线性定常系统状态方程的解

计算举例

Back to top