Skip to content

CH3. 系统的稳定性

总结

1 BIBO 稳定

系统 BIBO 稳定 \(\Leftrightarrow\) 系统全体可控可观模式/模态收敛.

  • 系统能控能观子系统的所有特征值均具有负实部
  • 复数域：传递函数极点全部在左半平面.

2 李雅普诺夫稳定

2.1 李雅普诺夫稳定的定义

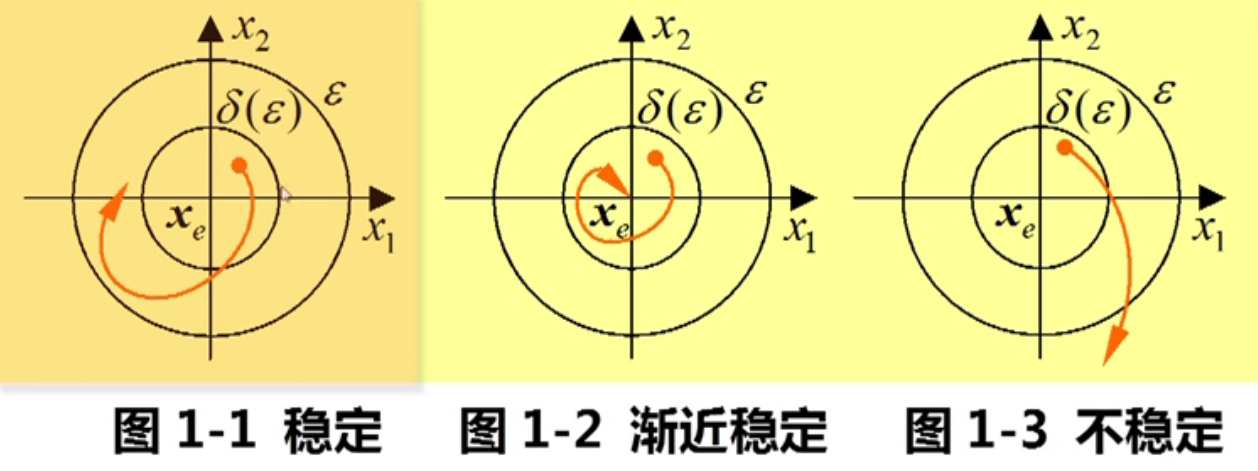
平衡态

平衡态指状态空间中状态变量的导数向量为零向量的点，因此平衡态指能够保持平衡，维持现状不运动的状态. \(\dot{x} = f(x,t)\equiv 0\), 记为 \(x_e\)

当矩阵 A 非奇异时，线性系统只有一个孤立的平衡态 \(x_e=0\)

对于非线性系统，通常有一或多个孤立平衡态，对应于 \(f(x,t)\equiv0\) 常值解.
对于其孤立平衡态，总是可以通过坐标变换将其移到状态空间的原点

因此，我们常把平衡态取为状态空间的原点.

2.2 李雅普诺夫方法

2.2.1 李雅普诺夫第一法，间接法：判断特征值

  • A 特征值均具有负实部，则渐近稳定；
  • 存在特征值具有正实部，则不稳定；
    对于非线性系统，可以将系统的描述在平衡点附近线性化，判断线性化模型 A 的特征值. 其他情况无法判断

可以这样理解，对于一个普通的一元函数，由泰勒公式有 \(y=f(x)=f(0)+f'(0)x+\cdots\).

而对于 \(\dot x_1=f(x_1,x_2)\), 一般来说原点处是平衡点，\(f(0,0)=0\). 则一阶展开能够得到 \(\dot x_1=f'_{x_1}(0,0)x_1+f'_{x_2}(0,0)x_2\).

\[ \begin{aligned} \dot x_1&=f'_{x_1}(0,0)x_1+f'_{x_2}(0,0)x_2\\ &=[f'_{x_1}, f'_{x_2}]|_{x=0}x \end{aligned} \]

总之，更成熟的表述方法应该是雅可比矩阵

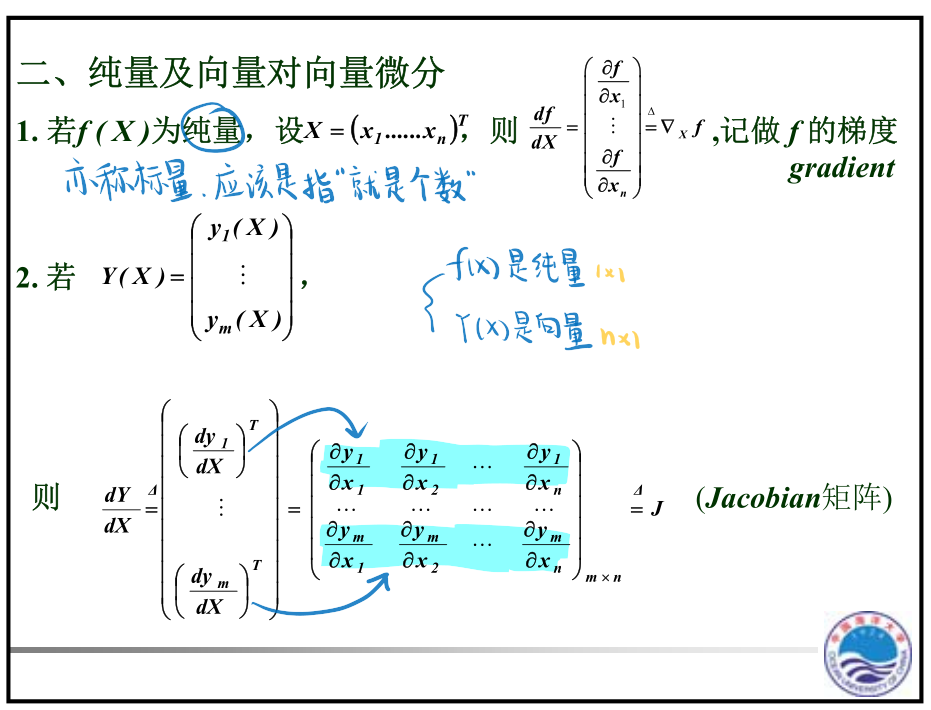
\[ A=\left. \frac{\partial f(x)}{\partial \boldsymbol{x^T}}\right|_{\boldsymbol {x}=\boldsymbol{x_e}}= \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \cdots&\cdots&\cdots\\ \frac{\partial f_n}{\partial x_1} &\cdots& \frac{\partial f_n}{\partial x_n}\\ \end{bmatrix}_{\boldsymbol{x}=\boldsymbol{x_e}} \]

课件上的雅可比矩阵

Example

2.2.2 直接法（第二方法）

2.2.2.1 判别标准

标量函数的定号性

  • 实函数正定性：对于任意 n 维非零向量 \(\boldsymbol{x}\in \Omega\)
    • \(V(x)>0, V(0)=0\) 正定
    • \(V(x)\ge0, V(0)=0\) 半正定
    • \(V(x)<0, V(0)=0\) 负定
    • \(V(x)\le0, V(0)=0\) 半负定
  • 矩阵正定性/二次型正定性：实对称矩阵 P

导数负定，相当于能量函数衰减

Attention

李雅普诺夫第二法给出的结果是充分条件，所以构造不出李雅普诺夫函数，只能说无法提供有关系统稳定性的信息，而不能说该系统不稳定

2.2.2.2 构造李雅普诺夫函数的方法

3 线性系统的稳定性分析

线性系统 BIBO 稳定 ⇒ 渐近稳定

使用方法：

  1. 选择单位矩阵 I 作为 Q
  2. 设 P, 通过等式 \(A^{T}P+PA=-Q\) 求 P
    这里没有什么很好的方法，好像只能设 p 每个位置的参数. 注意 P 是实对称矩阵！2x2 只需要设 3 个参数
  3. 判断顺序主子式是不是都大于 0 （矩阵是否正定）
  4. 如果正定，就渐近稳定，负定，就不稳定

理解&证明

线性定常系统状态方程为 \(\dot{x}=Ax\)
选取正定二次型函数、李雅普诺夫函数为 \(V(x)=x^TPx\)
则有 \(\dot{V}(x)=\dot{x}^TPx+x^TP\dot{x}=x^T(A^TP+PA)x=-x^TQx\)

《自动控制原理》（第六版）

一般地说求解李雅普诺夫方程并非易事，因而这种方法往往不用来判断系统的渐近稳定性，而是用来构造线性定常连续渐近稳定系统。

Back to top