自抗扰控制原理笔记

• 自抗扰控制原理笔记
  • 1 基本概念
  • 2 积分器串联型&总扰动
    • 2.1 进一步理解
  • 3 状态观测器&ESO
  • 4 线性自抗扰控制器 LADRC
    • 4.1 TD 跟踪微分器
  • 5 为什么研究自抗扰
  • 6 Furthermore

关于参考资料：在每个标题后面用引用的形式给出.
辅助基本概念理解… 可能有不准确的地方，再深入的推导证明啥的我就不费力写了

1 基本概念

高志强：何谓自抗扰？
自抗扰控制器（ADRC）学习笔记_哔哩哔哩

Cite

ADRC 是在 1990 年左右韩京清教授发明，在 PID 基础上做的一种创新。2003 年高志强教授在 ADRC 基础上，提出了简化版的 LADRC，将调解参数降为 3 个，极大方便了参数整定。学习 ADRC 有一个 B 站的公众号一定要关注一下，叫做：“自抗扰控制 ADRC”，是高志强教授在 B 站的做的科普账号，可以加到他们的 QQ 群里学习。

自抗扰控制 adaptive disturbance rejection

• 跟踪微分器 TD: 安排过渡过程并给出此过程的微分信号（指令和指令的微分都应该给控制器，这样能够更好跟踪指令）
• 扩张状态观测器 ESO: （感觉就是状态观测器，但是额外观测了一个总扰动） 把未知的扰动 f 估计出来，用控制器实时抵消掉，使控制系统接近理想对象（串联积分器）. 系统是二阶的，ESO 就是三阶的
  传统控制器是通过输出变化与输入做差，形成误差信号进行控制. ESO 是直接通过系统的输入输出观测到总扰动.
• 误差反馈控制，非线性组合：控制器用非线性的

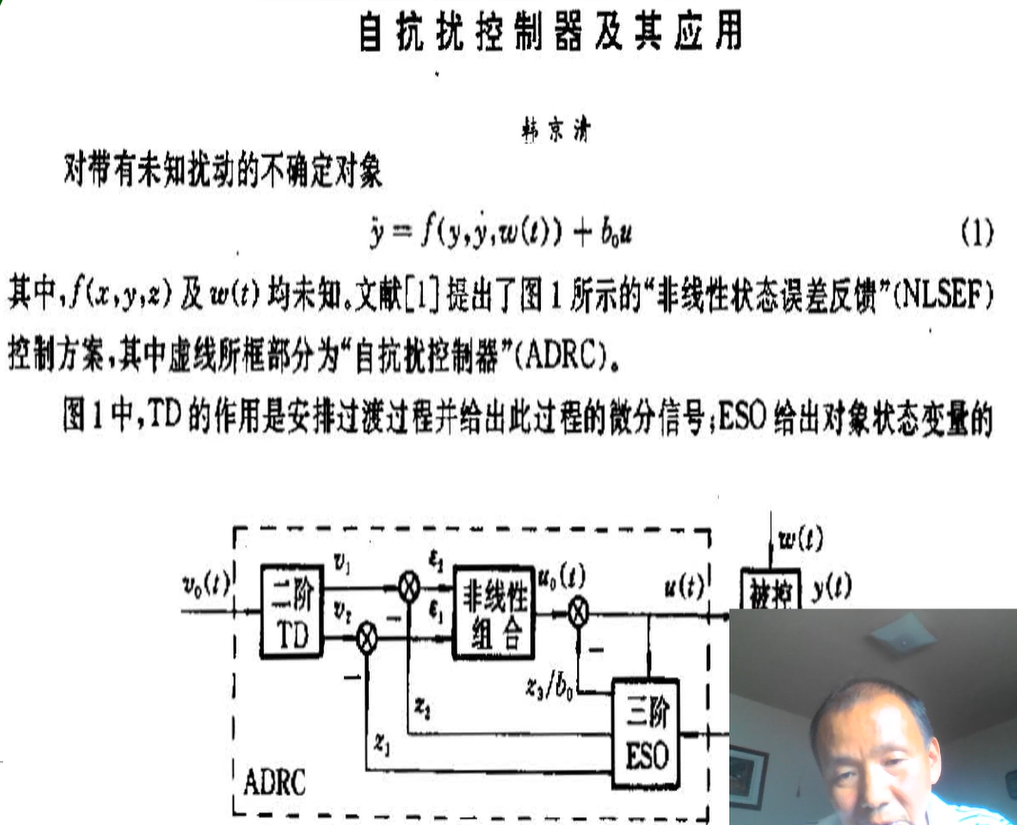
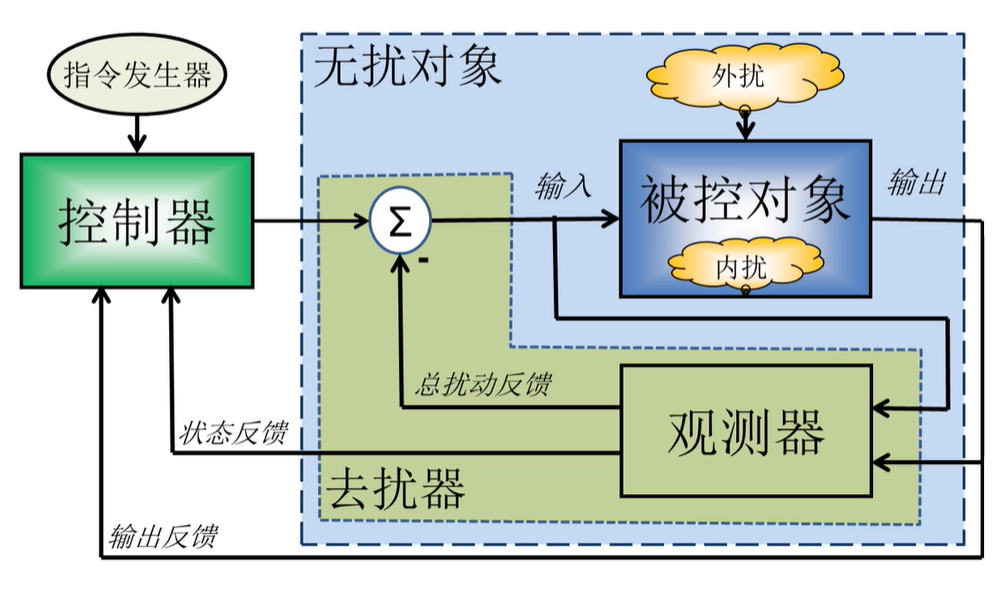
不确定 → 确定；
被扰动 → 无扰动

• \(b_0\) 物理量
• \(\omega_o\) 观测器带宽：观测器一定要能跟上扰动 f (f 在某个频域范围内）
• \(\omega_c\) 控制器带宽：一般教科书说\(\omega_c\approx\frac13\omega_o\)

三个参数不是盲目调的，要根据理解.

2 积分器串联型&总扰动

线性/非线性系统，在反馈的作用下，都可以回归于积分器串联型.
这样控制器基于积分器串联型设计就可以了。
注释：对于二阶积分器串联型，可以理解，\(y=\iint bu_0\), \(\ddot{y}=bu_0\)

二阶串联积分

对于一个典型的带阻尼弹簧力学模型，位移 s, 拉力 F, 有系统模型 \(\ddot{s}=\frac{F-k_1s-k_2\dot{s}}{m}\)
我们把后面的 \(\frac{-k_1s-k_2\dot{s}}{m}\) 当作扰动，想办法抵消掉，即令 \(F=F+k_1s+k_2\dot{s}\),
则系统关系将被转化为 \(\ddot{s}=\frac{F}{m}\), 即二层积分关系 \(G(s)=\frac{1}{m}\frac{1}{s}\frac{1}{s}\)
要构建 \(F=F+k_1s+k_2\dot{s}\), 我们需要知道 \(s, \dot s\) 这样的值，即观测状态，于是用到状态观测器. 实际上，引入总扰动的概念，则我们想要观测的只是总扰动 \(w=k_1s+k_2\dot{s}\) 这一个状态变量.

被控对象 = 积分器串联型 + 总扰动 （内外扰动）
用控制信号抵消掉总扰动，剩下的就是无扰动的标准型（积分串联型）, 针对这种简单形式的标准型设计控制器就简便很多。

2.1 进一步理解

我的理解: 积分器串联型简而言之就是说，输入是 u, 输出是 y, 那么对于 n 阶系统，有 \(y^{(n)}=bu\)
这里以三阶系统为例，有 \(y^{(3)}=bu\), 你可以设 \(x_1=y,\;\dot{x}_1=x_2,\;\dot{x}_2=x_3,\;\dot{x_3}=bu\)
写成状态空间方程为：

这里其实不用通过状态空间方程理解，但为了后面 ESO 部分和课本学习观测器设计串联，这里总结一下.

\[ \begin{cases} \dot{X}&= \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix}X + \begin{bmatrix} 0 \\ 0 \\ b \\ \end{bmatrix}u \\ y &= \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}X \end{cases} \]

当然实际系统往往存在扰动，并且不是串联积分的形式. 例如前面提到的有阻尼弹簧震动系统中 \(\ddot{s}=\frac{F-k_1s-k_2\dot{s}}{m}\).
这里以一个一般性的二阶形式为例 \(\ddot{x}=bu+a_1\dot{x}+a_0x+w\)
为不失一般性，末尾有 w 是未知的扰动.

那么这时候系统就可以写成：

\[ \begin{cases} \dot{X}&= \begin{bmatrix} 0 & 1 \\ a_0 & a_1 \\ \end{bmatrix}X + \begin{bmatrix} 0 \\ b \\ \end{bmatrix}u + \begin{bmatrix} 0 \\ w \\ \end{bmatrix} \\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix}X \end{cases} \]

写成这种形式后，我们通过把总扰动当作第三个状态变量，即 \(x_3= a_1\dot{x}+a_0x+w\), 则有 \(\dot{x}_2=bu+a_1x_2+a_0x_1+w=bu+x_3\) 令 \(\dot{x}_3=h\), 则系统状态空间方程为：

\[ \begin{cases} \dot{X}&= \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix}X + \begin{bmatrix} 0 \\ b \\ 0 \\ \end{bmatrix}u + \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix}h \\ y &= \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}X \end{cases} \]

这样就变成了刚开始的形式。.. (TODO) 唯一的问题可能就是，这里直接就写成了这样，而所有系统都能写成这种形式吗？好像没有证明.

原系统被视为 \(\ddot{x}=bu+a_1\dot{x}+a_0x+w=bu+f(\dot{x},x,t)+w(t)=\text{积分器串联型 + 总扰动}\)
\(f(\dot{x},x,t)\) 表示内部不确定动态
\(w(t)\) 表示外部未知扰动

3 状态观测器&ESO

基于视频 自抗扰控制器（ADRC）学习笔记 以及自己的理解进行下面的笔记. (TODO 不确定是否为官方思路..)
视频中是每个状态分开讲的，下面我是以设计伦伯格观测器的思路对 ESO 的设计进行的总结

Cite

重新建立状态观测器的概念是学习自抗扰控制必须迈过的一个台阶。控制专业的同学可能不理解，状态观测器的设计怎么能不依赖模型信息？非控制专业的同学和工程师们可能不理解，扰动信息是怎么实时估计出来的？

状态观测器：现代控制理论中，通过系统的输入输出估计系统状态 \(\hat{X}\) . 具体参考现控笔记中的"龙伯格观测器"

\[ \begin{cases} \dot{\hat{X}}=A\hat{X}+Bu+L(y-\hat{y})\\ \hat{y}=C\hat{X}+Du \end{cases} \]

\((y-\hat{y})\) 是一个观测得到的误差项，在之前的学习中，由于我们已知系统模型的全部信息，所以进行了进一步化简，将设计观测器问题转化为配置观测器的极点，即设计 \(A-LC\) 的特征根.
前面提到过 串联积分型的状态空间表达及其理解, 我的理解是，对于一个未知模型的系统，我们只需要知道阶数就可以构建出一个标准形态的状态空间方程.

\[ \begin{cases} \dot{X}&= \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix}X + \begin{bmatrix} 0 \\ b \\ 0 \\ \end{bmatrix}u + \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix}h \\ y &= \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}X \end{cases} \]

对于这样一种形式的系统进行观测器设计，有 \(y=x_1,\;y-\hat{y}=x_1-\hat{x}_1\) , 令 \(L=\begin{bmatrix}\beta_1&\beta_2&\beta_3\end{bmatrix}^T\) , 整理可得我们的观测器为：

这里有一种假设, 我也不太清楚，就是设计观测器时忽略掉了扰动 h 的作用，观测器仍可以逼近真实的状态）

\[ \hat{\dot{X}}= \begin{bmatrix} -\beta_1 & 1 & 0 \\ -\beta_2 & 0 & 1 \\ -\beta_3 & 0 & 0 \\ \end{bmatrix}\hat{X} + \begin{bmatrix} 0 & \beta_1 \\ b & \beta_2 \\ 0 & \beta_3 \\ \end{bmatrix}u\\ \]

\(|\lambda I-A|=\lambda^3+\beta_1\lambda^2+\beta_2\lambda+\beta_3=0\) 即为观测器的极点，例如配置成 \((s+\omega)^3\) 时，\(\beta_1=3\omega,\;\beta_2=2\omega_3,\;\beta_3=\omega^3\)

从这个角度来看，这种状态观测器的设计方法不需要除阶次以外的模型信息..

4 线性自抗扰控制器 LADRC

自抗扰控制器（ADRC）学习笔记_哔哩哔哩_bilibili

对于 \(\ddot{y}=bu\), 即二阶积分系统\(\frac{b}{s^2}\)进行控制，可采用 PD 控制器.
设给定值 \(sp\), 误差信号 \(sp-y\), PD 控制信号 \(K_p(sp-y)+K_d(sp-y)'\)
而 \(y,y'\) 都已经由 ESO 观测得到，因此只需要知道给定值及其微分，因此 ADRC 结构如下所示

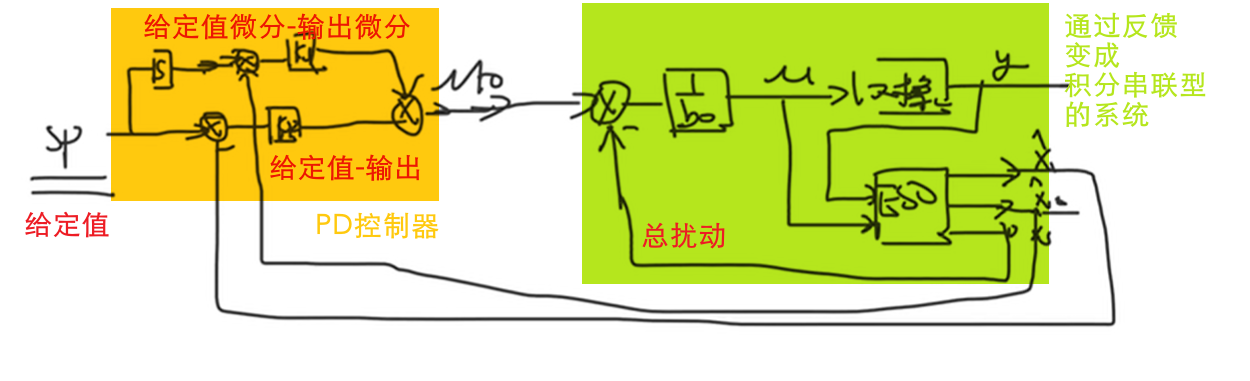
而实际上获得输入信号的微分不太方便，因此 ADRC 有一个 TD 跟踪微分器 可以很好地获得给定值的微分.
另外通过非线性组合模块实现\(sp-y\)及其导数的组合

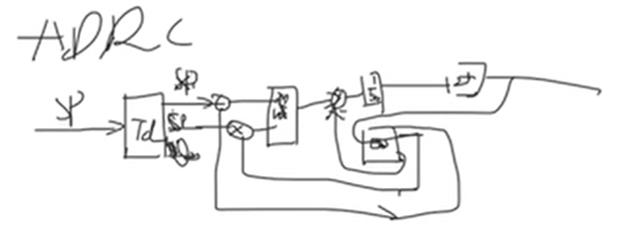
根据 自抗扰控制器（ADRC）学习笔记_哔哩哔哩_bilibili 里面的说法，在给定值是阶跃或者常值时，其微分为 0, 就简化为 LADRC

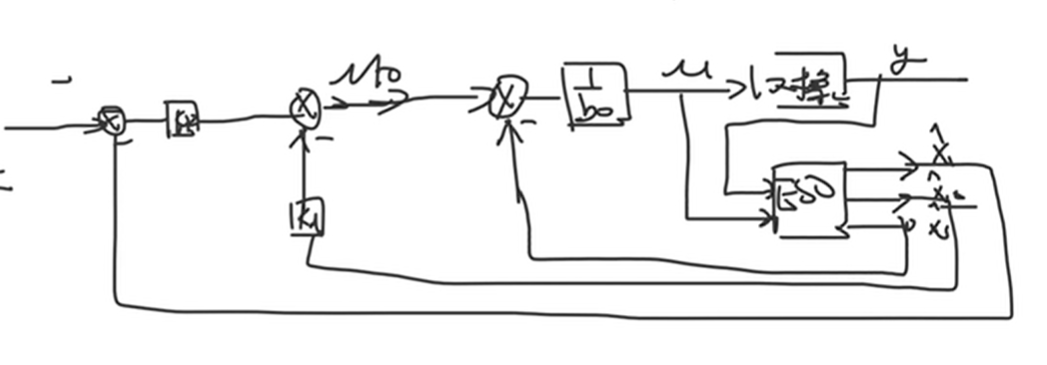
LADRC 是 ADRC 的一个特例

• LADRC 的整定参数只有三个 \(b_0,\omega_0, \omega_c\)
  • \(b_0\) 是由系统决定的，感觉有点像增益那个意思..?
  • \(\omega_0\)
  • \(\omega_c=\frac{\omega_0}{3\sim 10}\)
• ADRC 整定参数有 12 个

4.1 TD 跟踪微分器

\(\frac{s}{Ts+1}\) 实际可以造出来，模拟微分环节，但是对噪声很敏感.

5 为什么研究自抗扰

高志强：为什么要自抗扰？

工程控制本质问题

• 稳定性（十九世纪，起于天体力学：Airy, Maxwell, Lyapunov)
  
  
  瓦特设计蒸汽机，很多存在振动问题，引起对于稳定性的讨论研究

• 最优性（二十世纪，起于应用数学：LQ，\(H_{inf}\), …)

• 不变性、抗扰性、抗外扰（指南车，Poncelet 1829，Schipanov 1939, C.D. Johnson 1968，万百五
  1963, CCC 1979，关肇直 1980，韩京清 1981，Ohnishi 1983，…)
  

  

  使用一个快速响应的 Governor 应对蒸汽机的振动问题

  
  

  

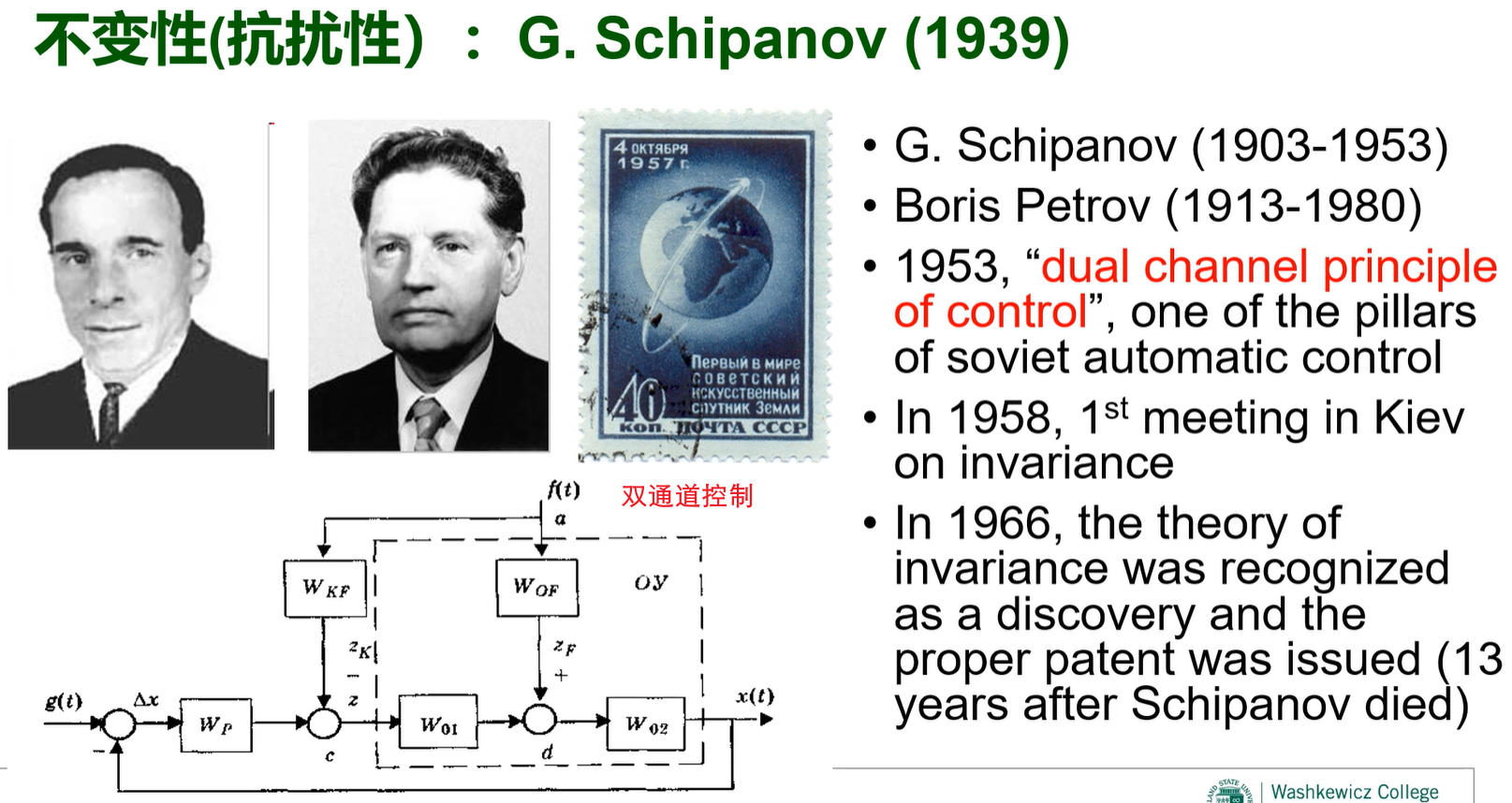
  俄国不变性理论

  
  

• 模型前提下的动态不确定性（抗扰控制，鲁棒控制，自适应控制，模型预测控制）

• 自抗扰：不基于模型，抗总扰动（内扰+外扰）（钱学森 1954，韩京清 1989，1998)

概念区分：

• 不变性理论、双通道原理、复合控制、抗扰控制：双自由度，添加对扰动信息的反馈
  
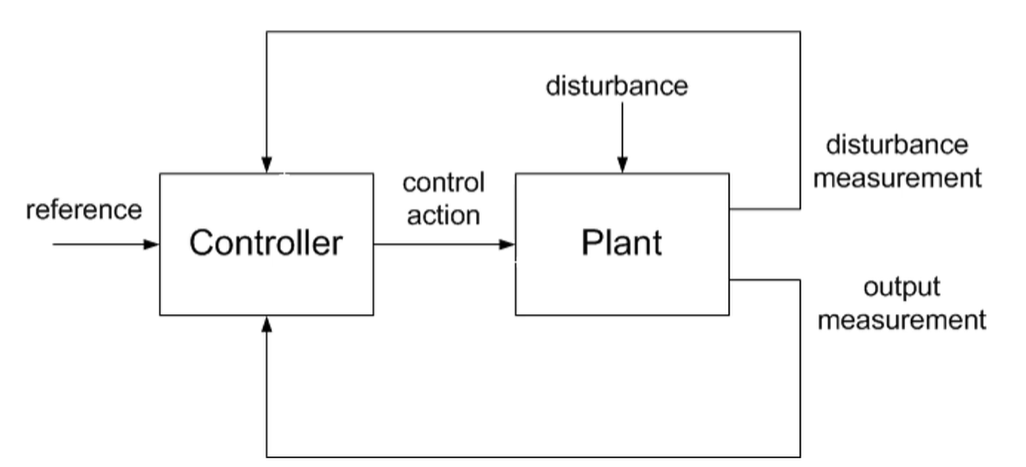
• 自抗扰性：和之前的抗扰不是一个概念，系统的动力学模型当作"内扰", 抵抗"总扰动"的"自抗扰控制器"是一个独立于模型的控制器（根据理想模型设计控制器）.
  

6 Furthermore

QQ 群：914841616
游客进入后群文件夹里找参考资料

https://www.bilibili.com/video/BV1ot4y1i7Af/?spm_id_from=333.788.recommend_more_video.1
https://www.bilibili.com/video/BV19v411q7Xi/?spm_id_from=333.788.recommend_more_video.3
https://www.bilibili.com/video/BV1fh41127Tw/?spm_id_from=333.788.recommend_more_video.18
https://www.bilibili.com/video/BV1yK4y1K7wB/?spm_id_from=333.788.recommend_more_video.4
自抗扰控制理论（三）线性 ADRC 的实现与仿真 - 知乎