第三章线性系统的时域分析法¶

如果生疏了，可以看看卢京潮的课，讲的很细，让人理解提高一个境界.

1 时域指标¶

稳：曲线不要发散（跟随给定）, 一般关注超调量 $\sigma \%$
准：稳态误差 $e_{ss}$
快：过渡过程，一般关注调节时间 $t_s$ （超调量尽可能小的同时，调节时间尽可能短）

2 一阶系统分析¶

\[\Phi(s)=\frac{1}{Ts+1}\]

超调量：无
调节时间：$t_s=3T$ ($5\%$误差带）

这个比较简单，如果从极点位置进行分析的话：
一阶系统有一个在实轴上的极点$-\frac{1}{T}$, 时间常数 T 越小，极点离虚轴越远，响应越快

3 二阶系统分析¶

一阶系统有一个自由度，有一个参数 $T$
二阶系统有两个自由度，有两个参数 $\omega_n, \xi$

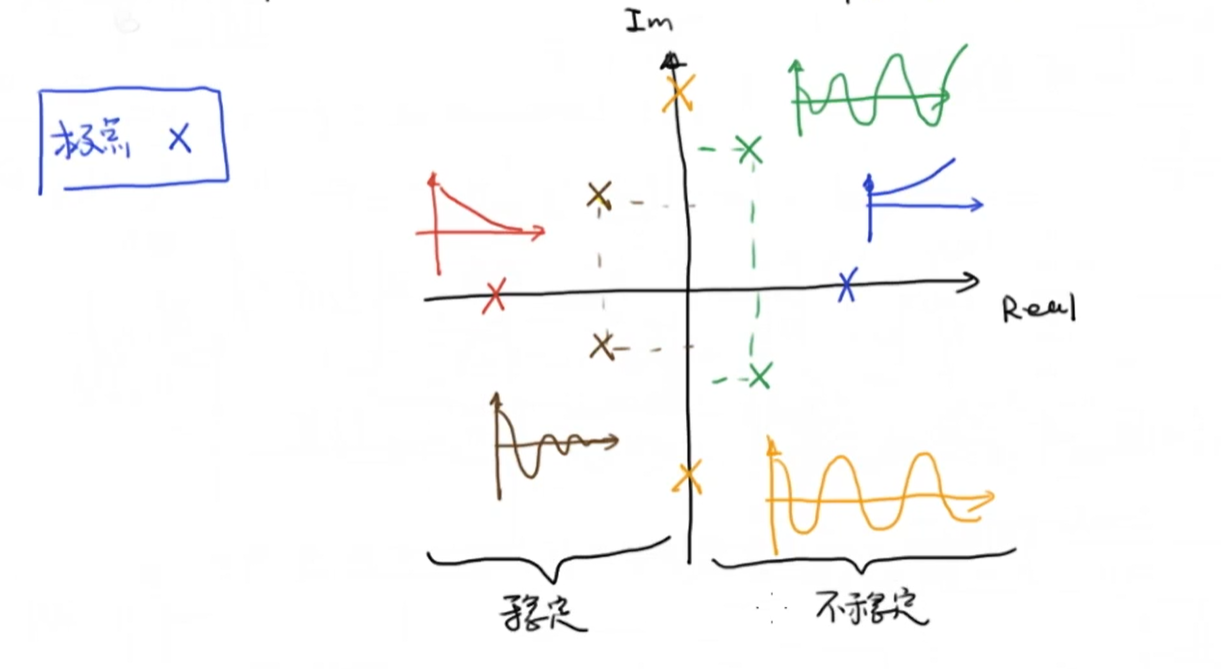
负阻尼，极点在右半平面
零阻尼，极点在虚轴
欠阻尼，极点在左半平面
临界阻尼，极点刚好位于实轴同一点处
过阻尼，极点在实轴

时域分析大体上，就是看极点位置对比，和根据现成公式计算时域指标
除了欠阻尼，这里并不单独讨论其他系统了，通过极点分析方法可以知道基本情况.

3.1 典型欠阻尼二阶系统¶

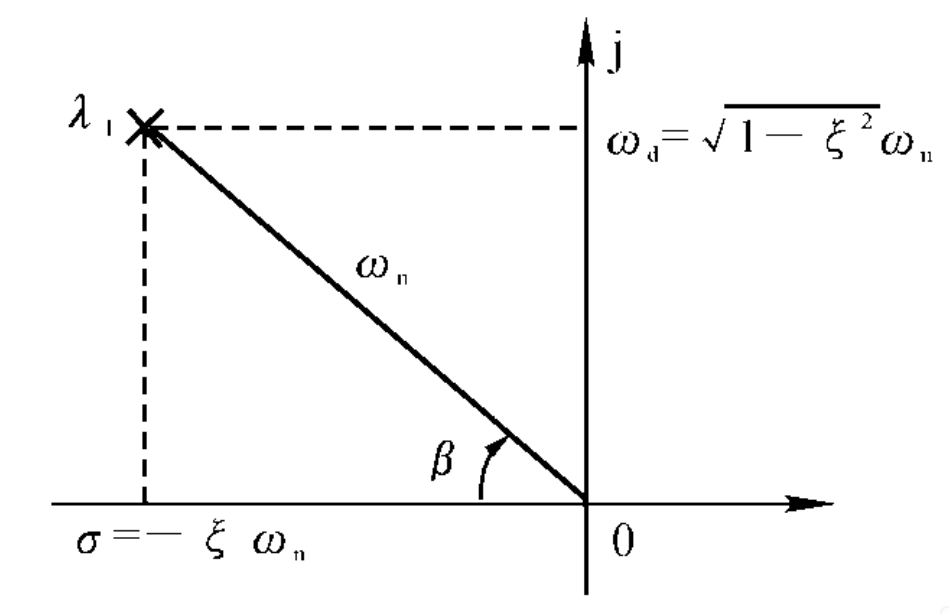
固有频率 $\omega_n$ 决定了极点所处圆的半径
阻尼比 $\xi$ 决定了极点所处的角度 $\cos\beta=\xi$
极点横坐标决定调节时间 $t_s=\frac{3.5}{\xi\omega_n}$ ($5\%$误差带）, $t_s=\frac{4}{\xi\omega_n}$ ($2\%$误差带）
极点纵坐标决定峰值时间

其他公式

有阻尼自然震荡角频率（也就是极点的纵坐标） $\omega_d=\omega_n\sqrt{1-\xi^2}$
上升时间 $t_p=\frac{\pi-\beta}{\omega_d}$
峰值时间 $t_p=\frac{\pi}{\omega_d}$

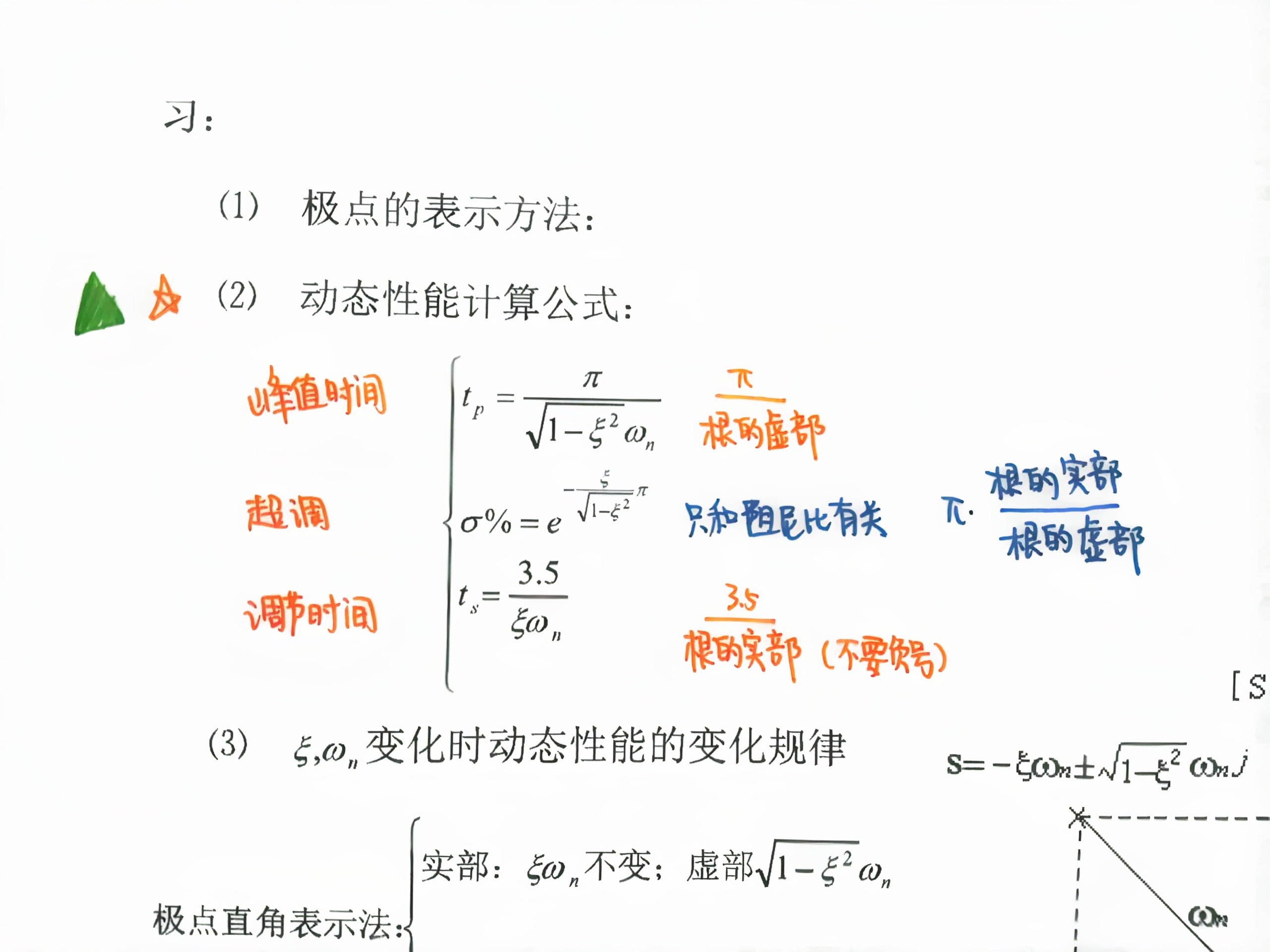
基本要求是理解极点位置对系统性能的影响
深入一些的话，就要熟悉曲线公式，记一下特殊位置的阻尼比了

理想的主导极点位置

远离虚轴，这样响应快；靠近实轴（或者沿 45°线）, 这样超调小（或者是）;
总之：希望极点位于 45°线，离虚轴尽可能远

往左：平稳性
往上：快速性

3.2 阻尼比¶

3.2.1 特殊阻尼比¶

3 个特殊的阻尼比，可以记一下，挺好记的，30,45,60, 超调差不多都和 4 有关，16, 5, 0.43

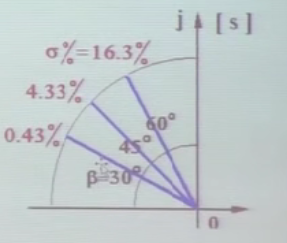
$\xi$	$\beta$	$\sigma\%$
0.5	60	0.43
0.707	45	4.33 （通常记为 `5%`误差 )
0.866	30	16.3

阻尼比 $\xi=1$时，刚好没有超调量，典型二阶系统可拆为 2 个惯性系统.

$s^2+2\omega_n^2 s+\omega_n^2=(s+\omega_n)^2$

直观理解：惯性系统拖慢系统，二阶过阻尼以及临界阻尼拖的比较厉害.

3.2.2 最佳阻尼比¶

为什么 最佳阻尼比 是 0.707?

固定$\xi\omega_n=C$ , 即极点实部不变，根据近似计算公式，调节时间不变. （前面按照包络线简化计算获得调节时间）
但是实际上，$\xi=0.707$ 处，调节时间 $t_s$ 最小.

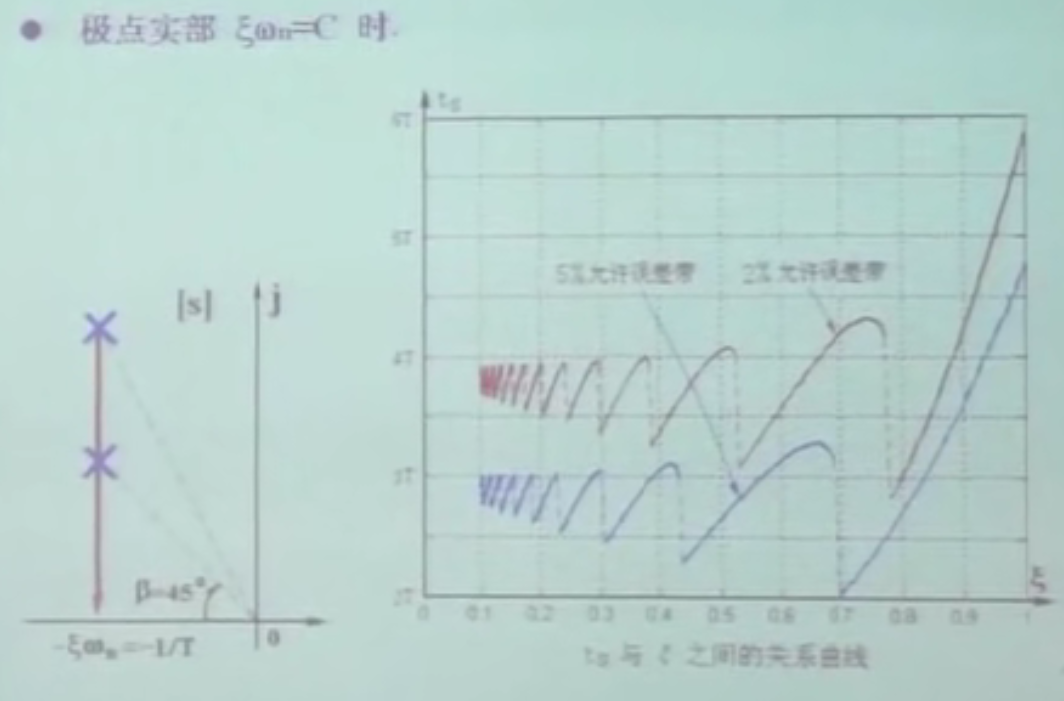
固定 $\omega_n=C$ 也能得出一样的结论.

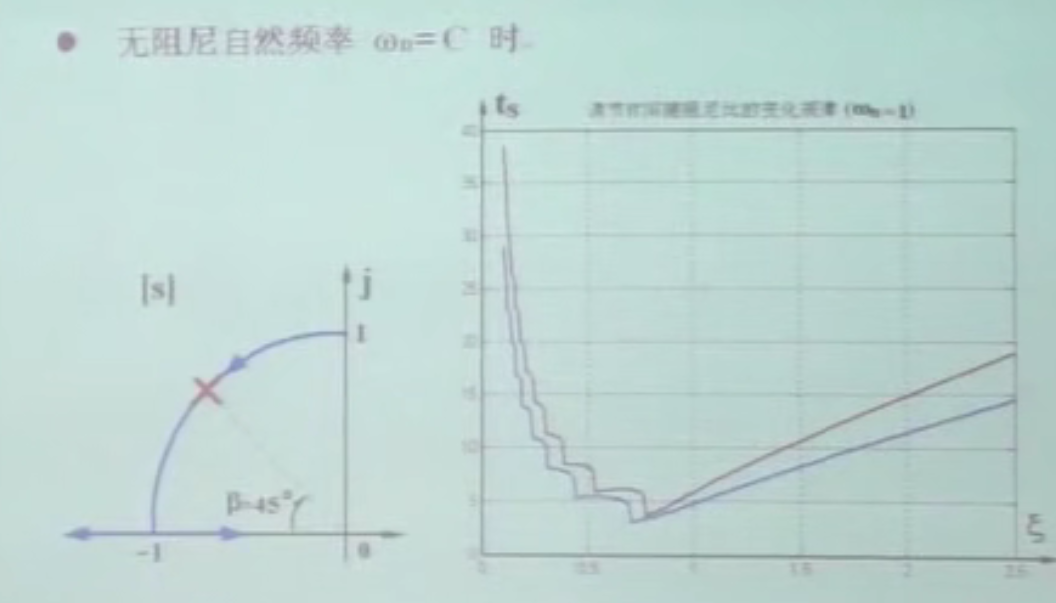
总结：

纯从理论研究来看，对于二阶系统来说，阻尼比为 0.707 时，实际调节时间最短，所以说是最佳.
超调 5%, 也不算很大
极点对应位置是 45°线上
我们希望系统极点位于 45°线上，离虚轴越远越好

对于最佳阻尼比 $\xi=0.707$,

带宽频率 $\omega_b=\omega_n$ 刚好出现共振
谐振频率 $\omega_r=0$
谐振峰值 $M_r=1$

3.3 其他¶

$\omega_n$
$\omega_d=\omega_n\sqrt{1-\xi^2}$
$\omega_r=\omega_n\sqrt{1-2\xi^2}$
$\omega_b=\omega_n\sqrt{1-2\xi^2+\sqrt{2-4\xi^2+4\xi^4}}$ （这个公式可能不需要记吧。)

4 高阶系统处理方法¶

4.1 主导极点法¶

舍去离虚轴远的，偶极子等，计算性能

主导极点
距离虚轴较近（收敛慢）, 对过渡过程影响较大的闭环极点.
> 离虚轴远的极点收敛快，只在响应初期起作用，对动态性能指标如调节时间影响不大
判断标准 : 距离虚轴的距离和其他极点差三倍距离/五倍距离/十倍距离以上）
偶极子
靠得很近，作用可以相互抵消的闭环零极点对（近似分子分母相消）
判断标准 : 零极点距离记为 $L_1$, 零极点离原点距离 $L_2$, 应该差 10 倍 $10 L_1< L_2$

Attention

舍去零点/极点后，其增益要保留下来
例如传函里是 $(s+p)$ 对应的极点被舍弃掉了，不是单纯地删去 $(s+p)$, 而是替换为 $p$, 这这样传递函数的增益不变.

4.2 零点极点法¶

如果舍去能舍去的东西之后，发现剩余的还是 2 阶以上，就使用零点极点法

上面的判断标准来自于卢京潮课程（或下载的讲义）, 其他地方没看到，应该不是铁律，只是一种经验.

Todo

零点极点法估算高阶系统第三章第十节

5 时域矫正：增加零极点¶

闭环极点决定响应的模态，闭环零点决定模态的加权系数.

Attention

这里指系统闭环零极点，即系统"最终的状态".
改变开环零极点属于"曲线救国", 需要在根轨迹那套体系里理解。

添加	影响
开环零点	从对根轨迹影响去理解，把根轨迹往左弯，并且零点还是根轨迹的终点，动态性能变好.
开环极点	从对根轨迹影响去理解，把根轨迹往右弯，不利于稳定性，动态性能变差.
闭环零点	从新增串联微分环节去理解，响应变快，超调增大，减小阻尼
闭环极点	从新增串联惯性环节去理解，响应变慢，超调减小，增大阻尼

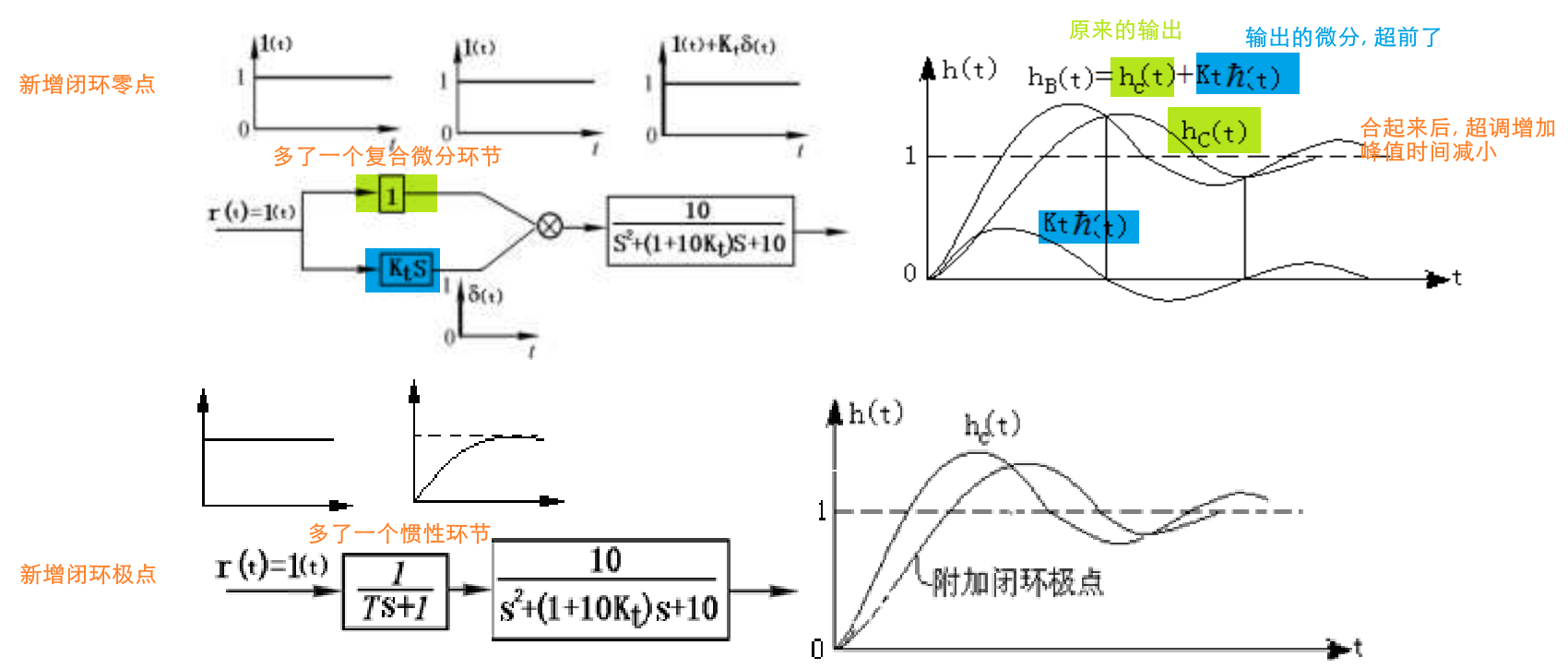
测速反馈添加了一个开环零点 $-\frac{1}{K_t}$, 使闭环极点位置左移动，增加了阻尼
附加闭环零极点离虚轴越近，效果越明显
附加开环零极点，一般指的都是串联校正，在闭环里面；附加闭环零极点，是加在反馈环以外，比如前置滤波

6 线性系统稳定性分析¶

经典控制理论认为临界稳定是不稳定，因此系统稳定的充要条件是，全部闭环极点落在左半 s 平面.

6.1 李一戚判据（必要判据）¶

特征方程系数不变号（都为正）
理解方式：$(s+p_1)(s+p_2)...(s+p_n)$ 根据排列组合，$s^k$的系数应该是 $n-k$ 个 $p_i$ 相加，如果极点都在左半平面，那么实部应该越加越大，不可能出现有的系数为正有的系数为负的情况.

6.2 劳斯判据（充要判据）¶

某行第一个元素是 0
原因（应该是）在于系统临界稳定. 虽然经典控制理论认为临界稳定（根的实部为 0) 不算稳定，但是劳斯判据判别的是特征方程存在正实部根的个数. 课程的处理为，这里不认为不稳定.
用一个很小的正数 $\epsilon$ 代替继续算
劳斯表中出现全零行
原因是特征方程中含有一些大小相等符号相反的实根或共轭虚根 (关于虚轴对称的根)。
处理方法: 利用系数全为零行的上一行系数构造一个辅助多项式，并以这个辅助多项式导数的系数来代替表中系数为全零的行，完成劳斯表的排列。
辅助多项式的根即为这些大小相等、符号相反的根，而且其根的数目总是偶数的。
注意, 辅助多项式只是表明特征方程有这些根，不能根据辅助多项式的次数判定有多少根，你可以通过长除法去掉这些对称的根后继续判断. （经验总结，可以看看下面这个例子）

如果发现存在纯虚根，说明临界稳定.

Example

系统特征多项式为：

\[ q(s)=s^{6}+3s^{5}+10s^{4}+24s^{3}+32s^{2}+48s+32 \]

7 线性系统稳态误差计算¶

7.1 定义法¶

计算稳态误差要先验证稳定性
一般误差信号会在方框图上标出来，可以根据梅森增益公式获得其表达式，之后利用终值定理判断稳态误差

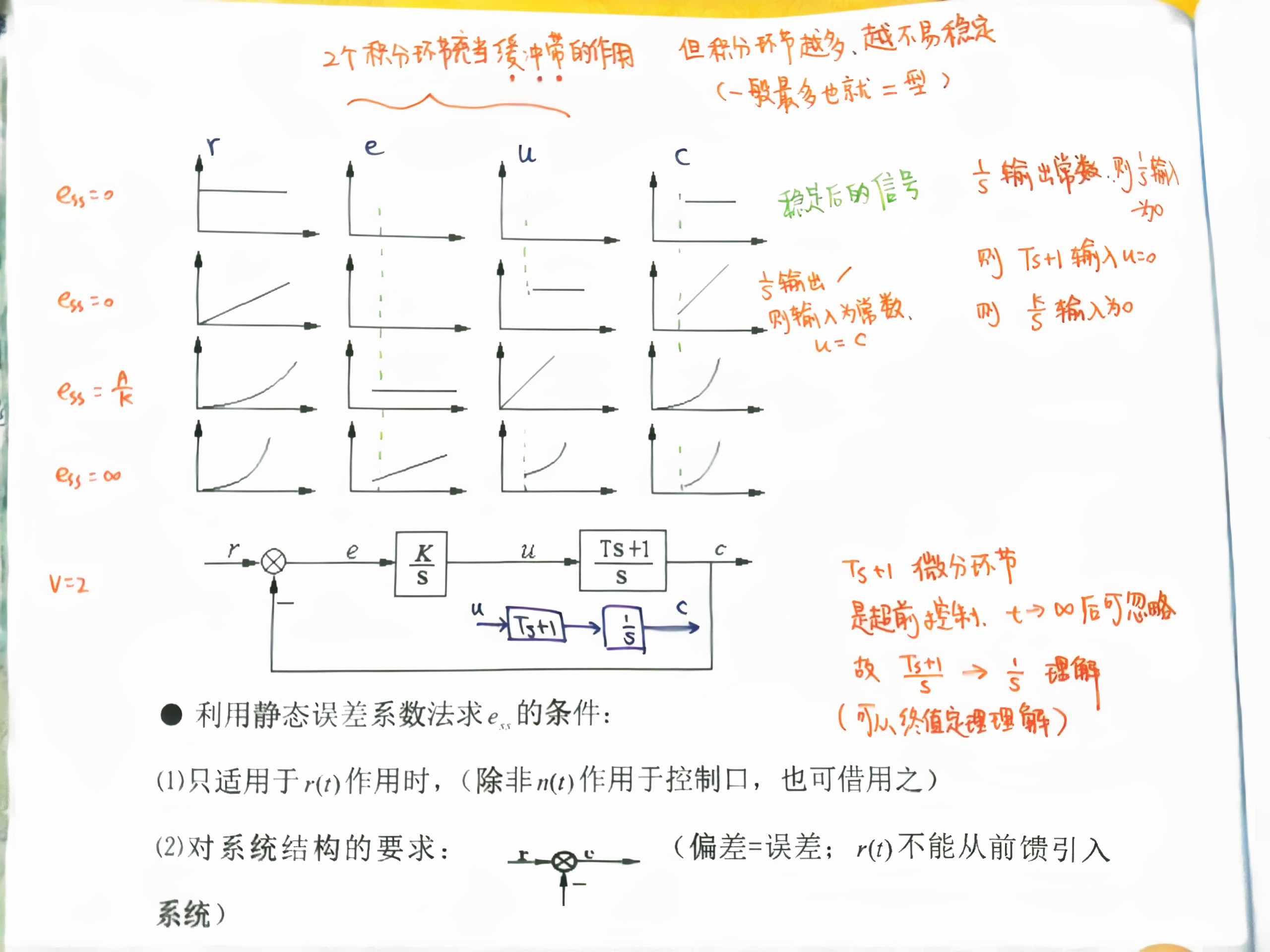
7.2 静态误差系数法¶

系统必须稳定
只适用于控制输入口加入信号（如果有前馈，就不能使用）
只对 E=R-B 定义有效（也就是说，误差的定义要在那个很常见的位置）
只适用于典型输入（大概）
位置输入 $A1(t)$
速度输入 $At$
加速度输入 $\frac{A}{2}t^2$

使用步骤：

求开环传递函数，判断开环增益 K, 系统型别 v
由输入阶数和输入幅值判断稳态误差

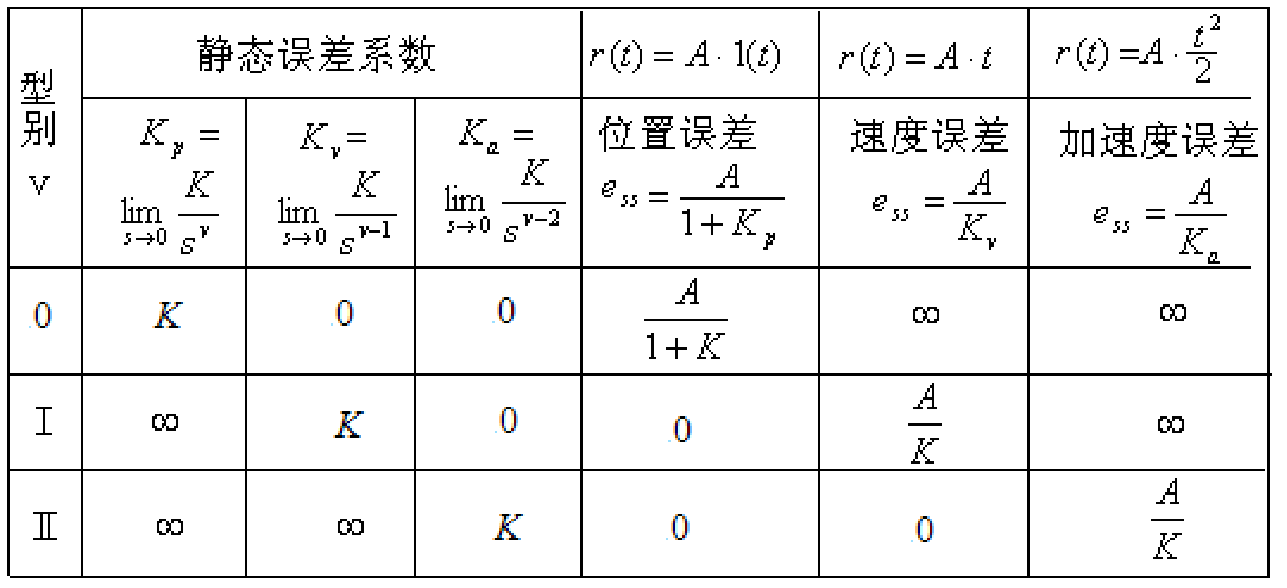
理解：积分环节是对跟踪能力的储备

增益对误差影响：

开环增益变大，则误差信号被放大，说明只需要维持很小的误差信号就能够实现较大的控制效果
闭环增益变大，只改变整体的幅值，不影响动态性能. 影响稳态值.

8 上课笔记¶

EXAM NOTIFICATION
动态性能指标没有大题. 动态性能指标公式不考，理解下定义就可以了.
一阶系统调节时间是三倍的时间常数
超调量只和阻尼比$\xi$有关，其他与$\xi,\omega_n$都有关

二阶系统要知道不同情况
极点计算公式需要掌握，公式里面的各个参数含义也需要清楚

$\xi,\omega_n$的不同情况
例如$\omega_d$有阻尼震荡角频率，$\omega_n$无阻尼震荡角频率？

极点位置与根轨迹结合考察，例如由根轨迹求临界稳定和临界阻尼时的 K 值.

稳定性劳斯判据一道大题 10 分
（不会考劳斯判据的稳定裕量）
要注意两种特殊情况，1 个数为 0 （取$\varepsilon$) 或者全 0 行

英语单词
误差 error
稳态误差 steady-state error

用英语写一下稳定的充分必要条件：
连续控制系统 (continuous control system) 稳定的充分必要条件 (necessary and sufficient conditions) 是闭环极点 (closed-loop poles) 都位于 S 平面 (S plane) 左侧.（离散控制系统稳定的充分必要条件是系统的特征方程的根都在 Z 平面以上以原点为圆心的单位圆内）
The sufficient and necessary condition for the stability of continuous control system is that all the closed-loop poles are located on the left side of the S plane.
All the closed-loop poles have negative real parts.
闭环系统特征方程的所有根均具有负实部
闭环传递函数的极点均位于 s 左半平面

稳态误差的几种定义

输入端定义
输出端定义
输入-输出

误差系数法求开环增益。填空题（倒数关系吧）

经典输入函数
工程上采用具有一定脉宽 b 和有限幅度的矩形脉动函数代替单位脉冲函数。b 要远小于系统时间常数 T，$b<0.1T$

时间常数表示过渡反应的时间过程的常数。
指该物理量从最大值衰减到最大值的 1/e 所需要的时间。对于某一按指数规律衰变的量，其幅值衰变为 1/e 倍时所需的时间称为时间常数。
$1/e=0.367879...\approx0.368$

填空题一阶、二阶微分方程与传递函数互相转换。
$\varPhi(s)=\frac{C(s)}{R(s)}$
知道传递函数、输入信号的 L 变换，可以推出$C(s)$，再反变换得到输出的时域微分方程。

传递函数典型环节总结：（根据分母 s 的阶数）

下面讲的“极点”指的是环节分母的根，“极点为正”说明传递函数极点在右半平面，系统不稳定。

典型环节可以看成构成任意系统的基本单元，典型环节的增益都是 1.

（负二阶）: $\tau^2s^2+2\xi\tau s+1$ 二阶复合微分环节
负一阶：$s$ 微分环节（一阶复合微分环节 $\tau s+1$)
零阶：$K$ 比例环节，放大环节
一阶
极点为 0：$\frac{1}{Ts}$积分环节 ($\frac{1}{s}$)
极点不为 0：$\frac{1}{Ts+1}$
- 极点为负：$T>0$ 惯性环节，惯性单元
- 极点为正：$T<0$ 不稳定环节
二阶
极点为负：$T>0,0\le\varsigma<1$
- 一般情况下：振荡环节 $\frac{1}{T^2s^2+2\xi Ts+1}$
- 当阻尼系数大于等于 1 时，二阶环节可以分解为两个惯性环节的乘积，不叫振荡环节。
极点为正：$T>0,-1<\varsigma<0$ 不稳定环节
特殊的滞后环节：$e^{-\tau s}$

实际系统都是因果系统，因此抽象成传递函数时，一般都是分子的阶数比分母低。因此典型环节中的微分环节实际不一定存在，只是用来单独进行分析。

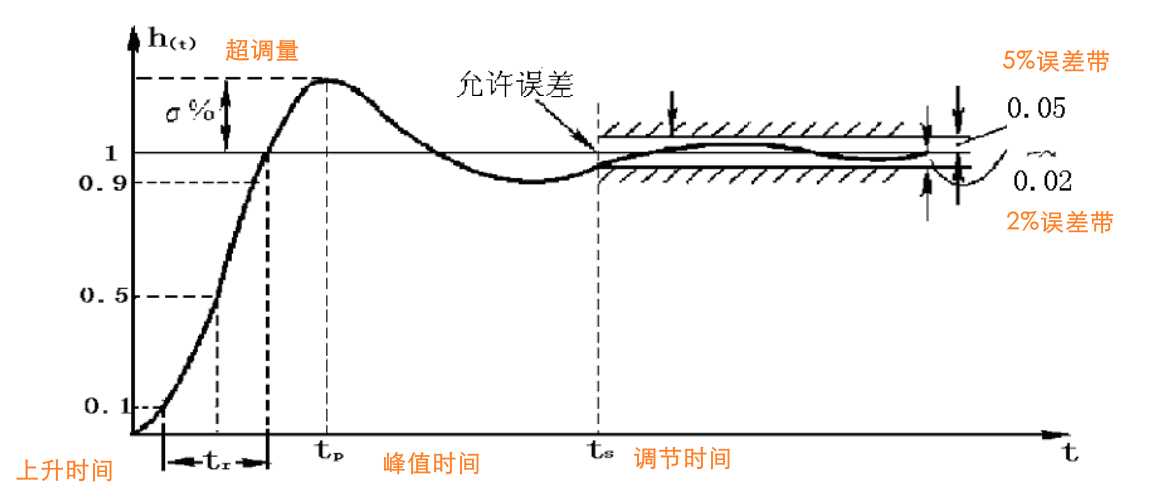
动态性能指标：

动态过程，动态性能指标
一般认为，阶跃输入对系统来说是最严峻的工作状态，通常在阶跃函数作用下（零状态），测定或计算系统的动态性能。
误差积分指标
上升时间 $t_r$：响应从终值 10%上升到 90%所需时间，对有震荡的系统，也可以定义为从 0 第一次上升到终值的时间。
峰值时间 $t_p$：响应超过终值达到第一个峰值的时间。
调节时间/过渡过程时间 $t_s$：响应到达并保持在终值上下 5%内所需时间。
超调量 $\sigma$：响应最大偏移量与终值的差与终值的比。
稳态过程，稳态性能指标
通常在阶跃函数，斜坡函数，加速度函数作用下进行测量。
稳定性
稳态误差

似乎只讲了阶跃响应的动态性能指标
阶跃响应重要性体现在，很多系统都是恒值调节系统。

关于动态性能指标的一些理解

一阶惯性系统$\frac{1}{Ts+1}$, 求调节时间（输出$0\to90\%h(\infty)$)$t_s=3T$（如果有延时环节再加上）填空题

自然震荡角频率$\omega_n$实际上是振荡环节波特图那个幅频特性的转折频率，因此表示了带宽的大小. 带宽大，自然动态性能就好，不管是上升时间，峰值时间，调节时间, 都会减少

阻尼增大了，调节时间会减小（到达稳态的能力）, 但是上升时间和峰值时间都是某种动态的能力，阻尼越小，越容易震荡，这两个值就越小.

超调量只和阻尼比有关，阻尼比越大，超调越小

系统总结

其实讨论几阶系统，相当于讨论系统的环节，一个高阶系统的内部可能有一部分/一个环节是低阶系统。

一阶系统
二阶系统：用的比较多，因为二阶平方项变化快。
高阶系统：没办法手算，所以不讲。
使用 MATLAB 仿真
（忽略远离虚轴的极点）近似成一阶或者二阶系统。

高阶系统的近似：
这部分是在第四章根轨迹法讲到的，通过观察零极点变化后对时间响应的影响，可以通过：取掉闭环偶极子之后，找到最接近虚轴的主导极点（一个实极点或者两个共轭极点）, 简化为一阶系统或者二阶系统进行分析.

二阶环节中阻尼系数$\xi$分析：

$-1<\xi<0$ 不稳定环节
$\xi=0$ 无阻尼（稳定不稳定的临界）
$0<\xi<1$ 欠阻尼
$\xi=1$ 临界阻尼（震荡不震荡的临界）
$\xi>1$ 过阻尼（可以分解为两个惯性环节，求出的两个根为实数）

（增加闭环）零极点对阻尼的影响：

增加零点有削弱阻尼的作用，越靠近原点，该作用越明显。
增加极点阻尼增大，越靠近原点，该作用越明显。

事实就是这样，小编也不知道为什么.

ATTENTION: 只能说附加的零极点对于阻尼的作用存在影响，不是简单的改变阻尼的值。
“阻尼越大”，超调量越小，上升时间减小。
但是调节时间不一定，可能增大可能减小（具体可以看 PDF 里面的图例）。

二阶系统：

\[ \varPhi(s)=\frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2}=\frac{1}{T^2s^2+2\varsigma Ts+1} \]

这个公式是二阶系统极点的计算结果要连同极点在复平面的分布背下来！
$$
s_{1,2}=-\xi\omega_n\pm j\omega_n\sqrt{1-\xi^2}
$$

无阻尼自振角频率/无阻尼震荡角频率：$\omega_n=\frac{1}{T}$（上边右边的传递函数中 s²项的系数的导数）
（有阻尼自振角频率，有阻尼震荡角频率）阻尼震荡角频率：$\omega_d=\omega_n\sqrt{1-\xi^2}$（极点纵坐标）

填空题：
已知$s=\pm2j$，求自然震荡角频率？
对照公式，易知$\xi=0$，无阻尼情况，$\omega_n=2$
考试：数学表达式不需要背，考试不会考记忆，重在理解。这部分不考计算题，所以可能会有画出大致极点分布之类的题目。

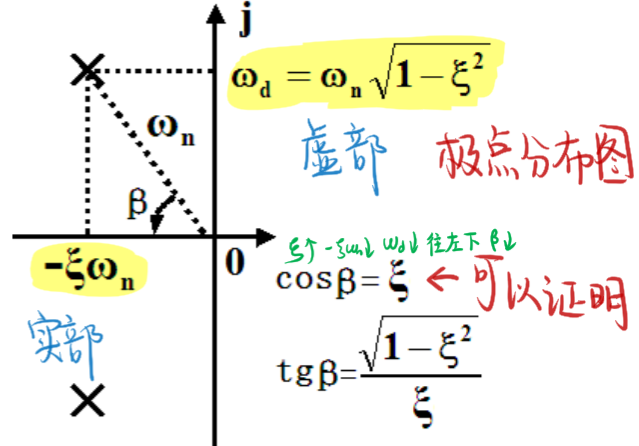
不同阻尼的情况下，极点的位置

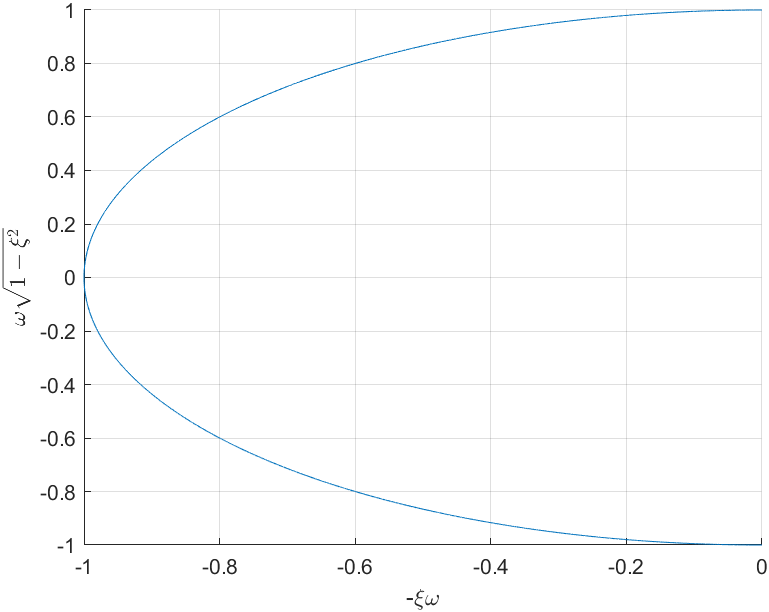
阻尼从 0 到 1, 开环极点从虚轴向左靠近实轴，最后归为 1 点. 再往后就是两个不等实极点了.
从这张图里可以看出阻尼越大，开环极点离虚轴越远.

xi=0:0.0001:1;
w=1;
x=-xi*w;
y=w*sqrt(1-xi.^2);
clf;hold on;
plot(x,y,"Color",[0 0.4470 0.7410]);
plot(x,-y,"Color",[0 0.4470 0.7410]);
grid;
xlabel -\xi\omega
ylabel("$$\omega\sqrt{1-\xi^2}$$","Interpreter","latex")

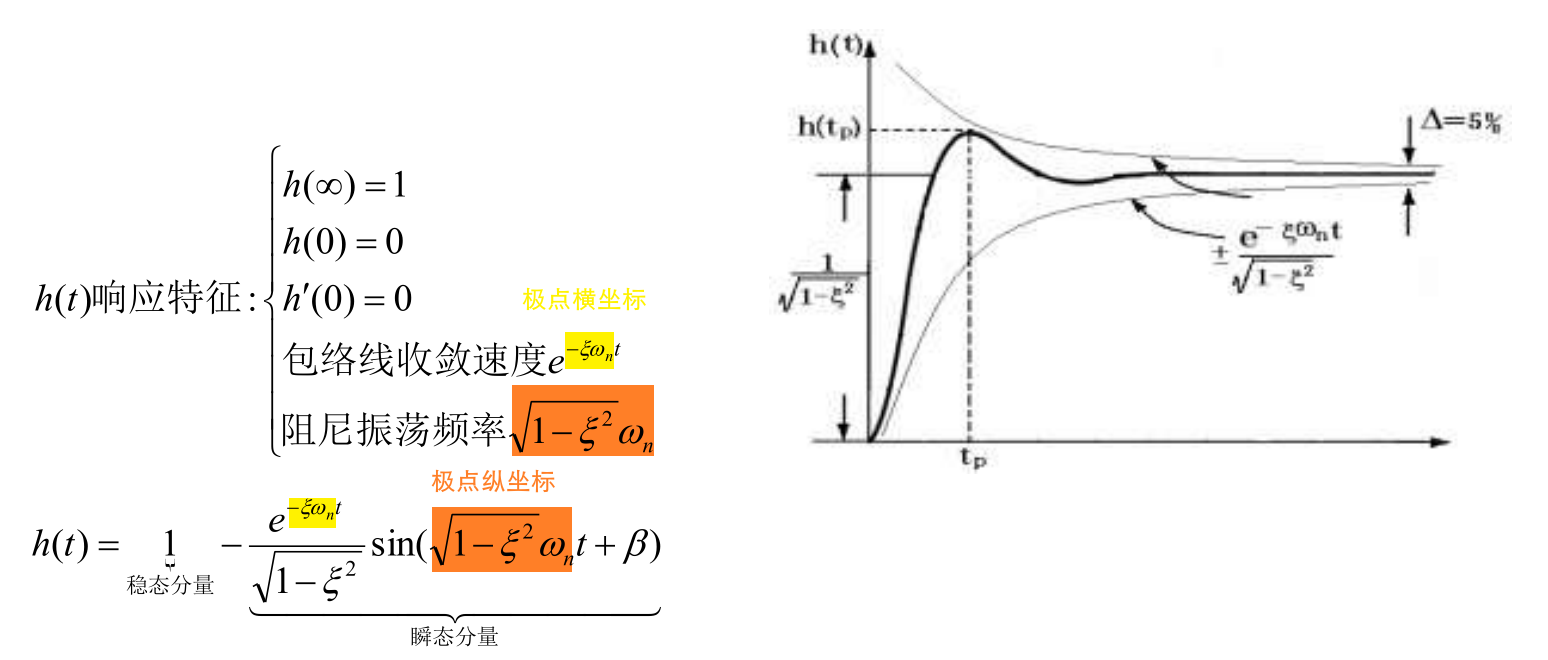
二阶系统 欠阻尼 动态性能指标（输入阶跃函数）：

上升时间 $t_r=\frac{\pi-\beta}{\omega_d}=\frac{1}{\omega_d}\arctan{\frac{\sqrt{1-\xi^2}}{-\xi}}$
峰值时间 $t_p=\frac{\pi}{\omega_d}=\frac{\pi}{\omega_n\sqrt{1-\xi^2}}$
超调量 $\sigma=c(t_p)-1=e^{-\frac{\xi\pi}{\sqrt{1-\xi^2}}}$
调节时间/过渡过程时间 $t_s\approx\frac{3}{\xi\omega_n}=\frac{3T}{\xi}$ (5%)

从课本 P75 二阶系统单位阶跃响应曲线
阻尼越大震荡越小，同时过阻尼状态后没有震荡。
需要注意的是，过阻尼状态时，调节时间较长，系统响应缓慢，并且阻尼越大，调节时间越长，这点课本/课堂上没有给出证明。
（这一块在课本 P79)

控制工程中，除了那些不容许产生振荡响应的系统外，通常都希望控制系统具有适度的阻尼，较快的响应速度，较短的调节时间。因此二阶系统一般 $\xi=0.4\sim0.8$

对比不同系统的性能：

直接法：计算出时域函数，通过完整的曲线进行对比
间接法：通过某几项性能指标进行对比。

比如说：先通过超调量$\sigma$确定$\xi$, 则可以对比出稳定性，然后再确定$\omega_n$

稳定性分析：

稳定性的定义：李雅普诺夫稳定性定义

正反馈通常是不稳定的，负反馈不一定稳定。
填空题

线性系统稳定性与初始状态无关
特征方程的所有跟均具有负实部（实部为 0 的纯虚根不被当做稳定，经典控制理论中，只有渐进稳定的系统才称之为稳定系统）时稳定。
极点均位于左半平面时稳定。
非线性系统稳定性与初始状态有关

将问题转化为：“如何判断一个方程有没有右根？”

线性定常系统稳定性分析方法：

劳思—赫尔维茨判据（Routh—hurwitz）
根轨迹法
奈魁斯特判据（Nyquist）

利用 MATLAB 进行控制系统稳定性判别的方法：

直接判别法：连续系统闭环极点都在 S 平面的左半平面，离散系统闭环极点都位于 Z 平面的单位圆内.

绘制零极点图判断

绘制时域响应曲线（单位阶跃、单位脉冲等）判断

劳斯判据 10 分大题
不会很难，算错其中一步导致最后结果错了的话，只扣那一步的马虎分。

初步筛选：如果存在$a_i\le0$必不稳定。
对于二阶系统，如果$a_i>0$，则系统是稳定的（充分必要条件）。
对于一般系统，则是稳定的必要条件，即不一定稳定，还需要进一步判断。

$$
s_{1,2}=-\xi\omega_n\pm j\omega_n\sqrt{1-\xi^2}
$$
对于二阶系统，只要阻尼$\xi>0$则系统稳定，参考$s^2+2\xi\omega_ns+\omega_n^2=0$，$2\xi\omega_n>0$时根一定都有负实部，阻尼一定大于 0，所以一定稳定。
列劳斯行列表
判断
第一列全部为正是稳定的充分必要条件。
第一列符号改变次数为右半 s 平面极点数。

有纯虚根或者关于原点对称的根，会出现全 0 行。

劳斯判据本质上就是求一个多项式右根数目。因此在后面频域法之类的也可以用.

稳态误差：

稳态误差$e_{ss}$的三种定义方式

$E(s)$如果在题目的系统框图里标了，一般就是标在$R(s)$后边，这时是从输入端定义稳态误差。
如果没有标，那就不知道了，但是从输入端定义更符合直观感受，感觉更常用一些.
单位负反馈时，三种定义相同！

输入端定义$E(s)=R(s)-C(s)H(s)$
输出端定义$E(s)=\frac{R(s)}{H(s)}-C(s)$
其他$E(s)=R(s)-C(s)$

计算稳态误差：使用拉氏变换的终值定理。（很简单，所以重点就是列稳态误差表达式）.

使用终值定理的时候要看值是否存在，如果不存在，可能算出一个数，但是是不对的。
体现在自控原理求稳态误差上，应该是先判断稳定性吧.

在列写稳态误差表达式时，需要注意题干中的条件：稳态误差定义类型，提供的"传递函数"类型，反馈类型（单位负反馈）以及是否有扰动（感觉可以使用梅森增益公式计算）。

闭环系统的闭环传函$G_c(s)=\frac{G(s)}{1+G(s)H(s)}$
闭环系统的开环传函$G_0(s)=G(s)H(s)$
闭环系统系统框图中的$G(s)$

减小或消除误差的方法：

增大系统开环增益或扰动作用点之前系统的增益。
在系统的前向通道或主反馈通道设置串联积分环节。（只要串的够多，分分钟稳态误差为 0）
采用串级控制抑制内回路扰动。
采用复合控制方法。

详见 PPT：
误差输入来源有$R(s),N(s)$
针对某一个特定输入，将其他输入置零，求这个输入与误差 E 的关系，$E_r(s),E_n(s)$

全补偿：令$E$的分子为 0，这样全过程且任意信号形式都没有误差。结果是精确的一个。
稳态补偿：对$E$使用终值定理，使稳态误差为 0，这种方法需要知道信号形式，结果有无限个。因为只规定了传递函数的增益，可以任意增加零极点。

没有扰动下的稳态误差计算（从输入端定义）：
一般公式：

下面使用单位负反馈举例：$H(s)=1,E(s)=R(s)-H(s)$

闭环系统的闭环传函
$E(s)=R(s)-C(s)=R[s](1-\frac{C(s)}{R(s)})=R[s](1-G_c(s))$
闭环系统的开环传函
$E(s)=\frac{R(s)}{1+G(s)}=\frac{R(s)}{1+G_0(s)}$
闭环系统系统框图中的$G(s)$
$E(s)=\frac{R(s)}{1+G(s)}$

背景知识：

输入函数$R(s)$为单位阶跃函数、单位斜坡函数、单位加速度函数，没有讲更高阶得了。这里我为了总结普遍规律，将它们表示为$R(s)=\frac{1}{s^{\alpha}},\alpha=1,2,3,...$，$\alpha\uparrow$输入变化越快，输出越不容易稳定。
系统传递函数$H(s)$采用归一式/时间常数式，此时有$\lim_{s\to0}H(s)=K$开环增益/开环比例系数可以直接从表达式看出来，K 越大系统越稳定。
另外零极点个数设为$\gamma$个，此时系统为$\gamma$型系统，有$\gamma$个积分环节，$\gamma\uparrow$系统越不容易稳定，但是稳定的话稳态误差越小。

\[ e_{ss}=\lim_{s\to0}sE(s) =\lim_{s\to0}\frac{sR(s)}{1+G_0(s)} =\lim_{s\to0}\frac{\frac{1}{s^{\alpha-1}}}{1+G_0(s)} =\lim_{s\to0}\frac{1}{s^{\alpha-1}(1+G_0(s))} \]

考试中，求稳态误差需要先判断是否稳定，不然计算出来的结果没有意义。
然后一般就这三种了，如果要归纳一般结论的话：
（从上面列的式子可以很容易理解）

$\alpha-1=\gamma$时

静态误差系数为$K$

稳态误差为$1/K$

$\alpha-1<\gamma$时

静态误差系数为$\infty$

稳态误差为$0$

$\alpha-1>\gamma$时

静态误差系数为$0$

稳态误差为$\infty$

$\gamma$	$K_p=\frac{K}{s^\gamma}/e_{ss}$	$K_v=\frac{K}{s^{\gamma-1}}/e_{ss}$	$K_a=\frac{K}{s^{\gamma-2}}/e_{ss}$
0	$K/\frac{1}{1+K}$	$0/\infty$	$0/\infty$
1	$\infty/0$	$K/\frac{1}{K}$	$0/\infty$
2	$\infty/0$	$\infty/0$	$K/\frac{1}{K}$

分析举例：
参考课本上一阶系统的分析：

单位脉冲响应：
$c(t)=\frac{1}{T}e^{-\frac{t}{T}}$
稳态误差为 0
单位阶跃响应：
$c(t)=1-e^{-\frac{t}{T}}$
稳态误差为 0
单位斜坡响应：
$c(t)=(t-T)+Te^{-\frac{t}{T}}$
稳态误差为 T
单位加速度响应：
$c(t)=\frac{1}{2}t^2-Tt+T^2(1-e^{-\frac{t}{T}})$
跟踪误差随时间推移而增大至无限，因此一阶系统不能实现对加速度输入函数的跟踪。

考虑误差扰动的稳态误差计算

题目中会给一个系统框图，标出各个扰动作用的位置。一般情况下（我就做了一道题），会标出E(s)的位置。
这种情况下，只需要根据梅森增益公式的思想得到$R(s),N_i(s)$到$E(s)$的传递函数就可以了。
利用叠加定理可以获得共同作用的稳态误差。

如果不标$E(s)$的话，以后遇到题目再整理吧。

\(\gamma\)	\(K_p=\frac{K}{s^\gamma}/e_{ss}\)	\(K_v=\frac{K}{s^{\gamma-1}}/e_{ss}\)	\(K_a=\frac{K}{s^{\gamma-2}}/e_{ss}\)
0	\(K/\frac{1}{1+K}\)	\(0/\infty\)	\(0/\infty\)
1	\(\infty/0\)	\(K/\frac{1}{K}\)	\(0/\infty\)
2	\(\infty/0\)	\(\infty/0\)	\(K/\frac{1}{K}\)

第三章 线性系统的时域分析法¶