薛文超 自抗扰控制¶
薛文超 自抗扰控制 (1)_哔哩哔哩_bilibili
薛文超 自抗扰控制 (2)_哔哩哔哩_bilibili
1 自抗扰控制核心思想¶

- 基于模型:利用数据辨识不确定动态和干扰 → 成本高,非线性辨识理论难,时变
- 自抗扰:把不确定性当成信号的一个微分看待而非一个非线性模型,关心不确定性组合的实时值 → 把总扰动当作一个状态进行观测

2 扩张状态观测器地数据驱动机制及应用¶
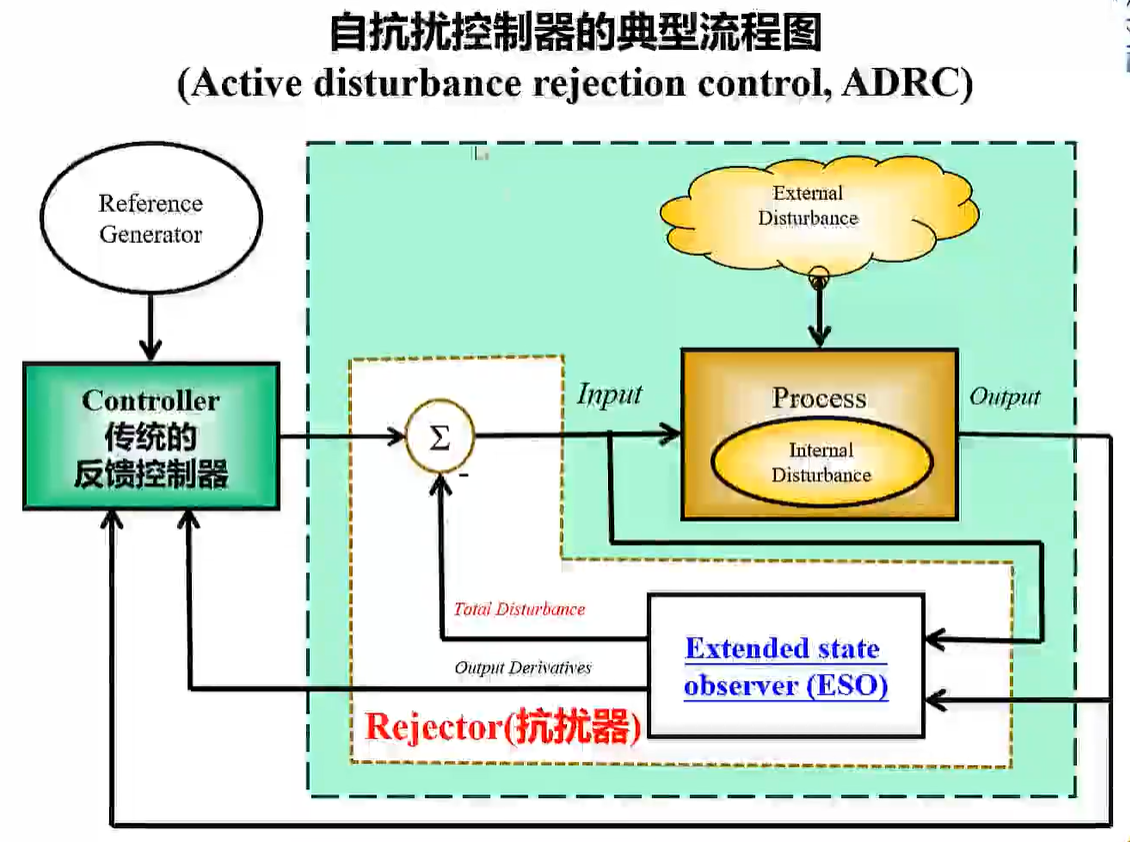
从一个更宽泛的角度来说,ESO 观测得到扰动并补偿掉,系统就简化为了我们的已知部分. 我们通过抗扰器把时变的、不清楚的部分补偿掉,之后就可以使用传统的控制方法. (高志强)
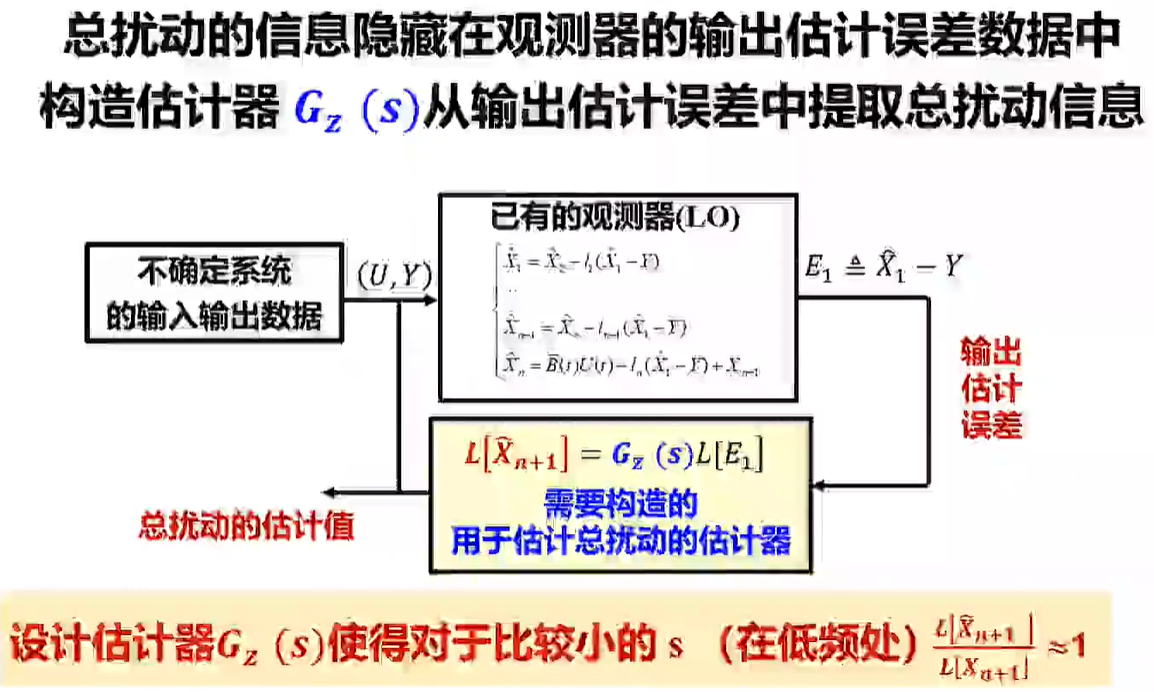
对不确定系统进行观测器设计

总扰动的信息隐藏在观测器的输出估计误差之中。
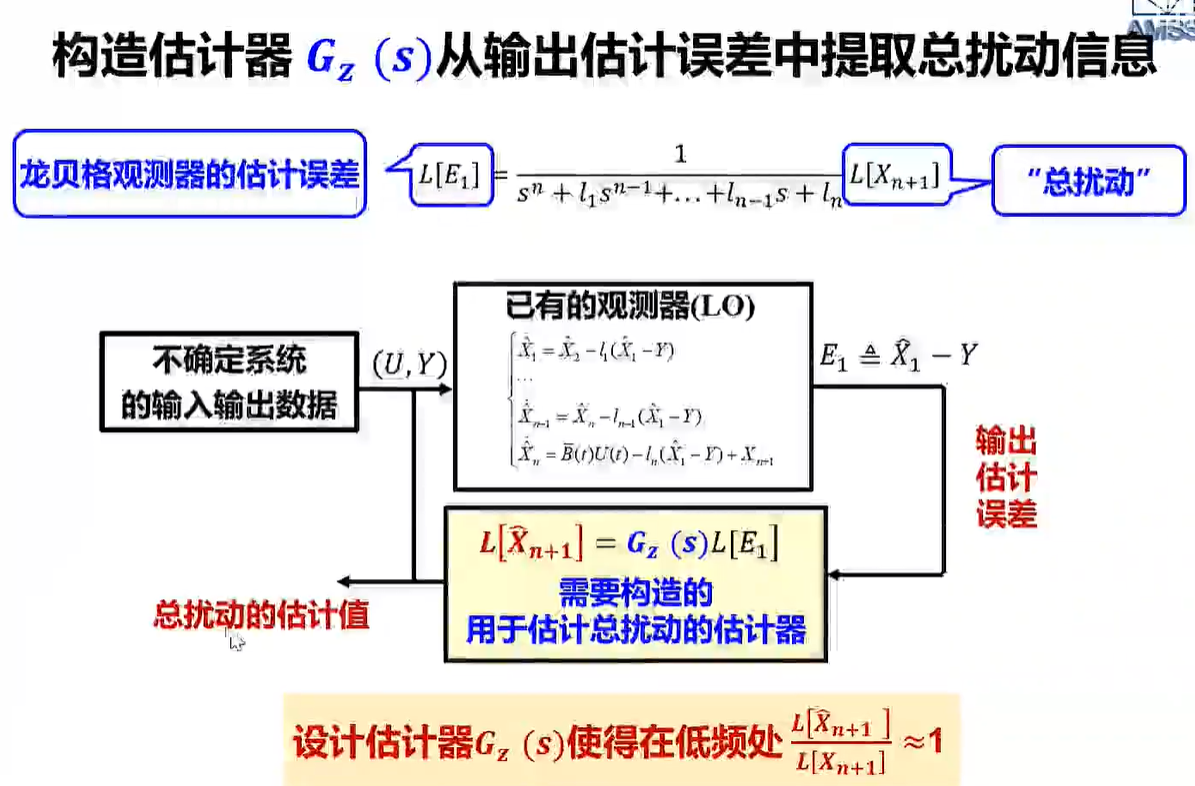
扰动相对来说还是低频的,因此扰动估计器的传递函数应该在低频处接近 1

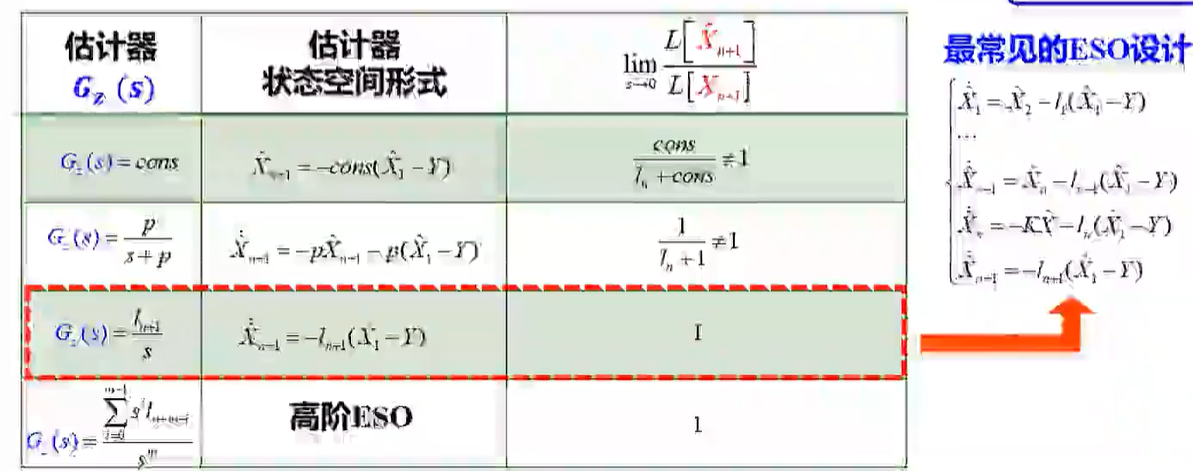
最常见的 ESO 设计就是把传统观测器的估计误差拿过来做了一个积分. 从理论上看,误差-估计误差 的传递函数确实在低频处等于 1, 表明可以估计出低频的扰动信号.
这个部分在 自抗扰控制原理笔记.md 的 ADRC 学习笔记视频链接里面提到过.
Add-On Module of Active Disturbance Rejection for Set-Point Tracking of Motion Control Systems
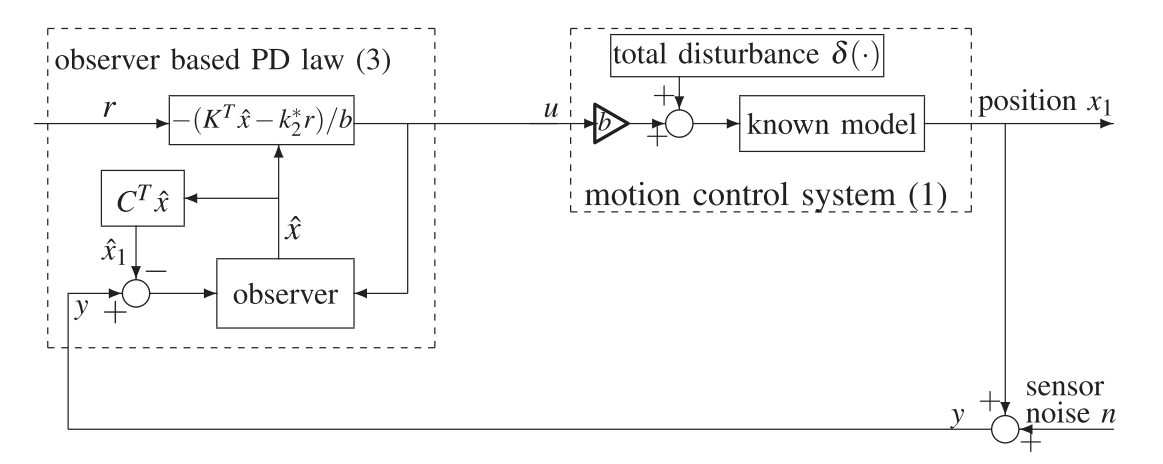
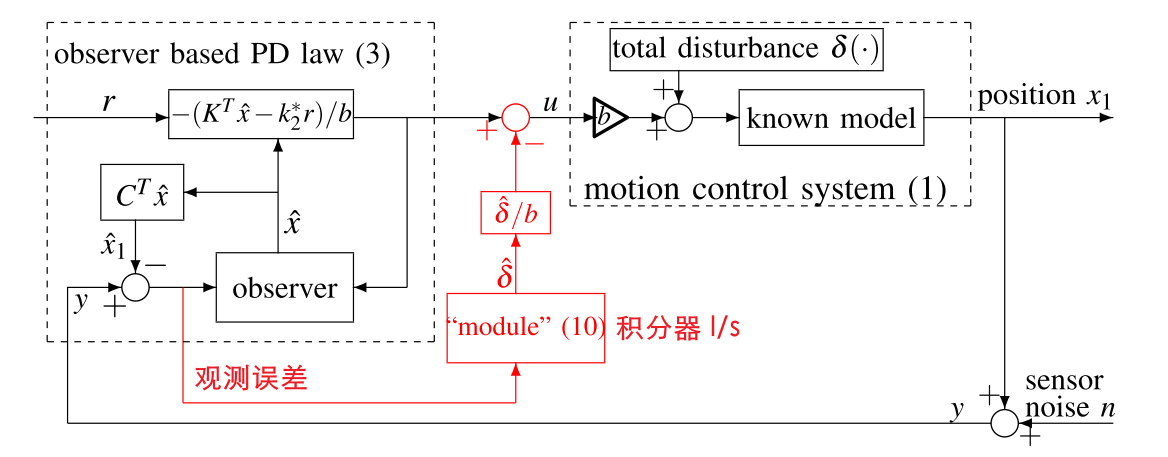
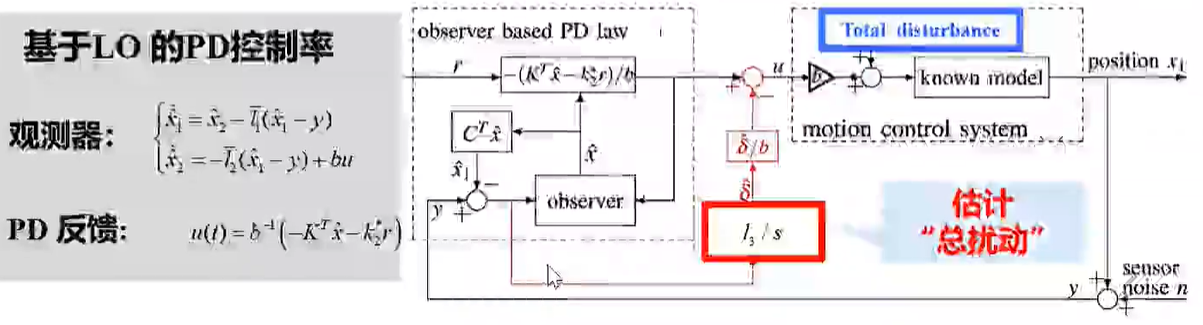
- 用数据驱动的方法估计和消除不确定性
- 不改变原来的控制回路
- 在低频处有更好的抗扰能力
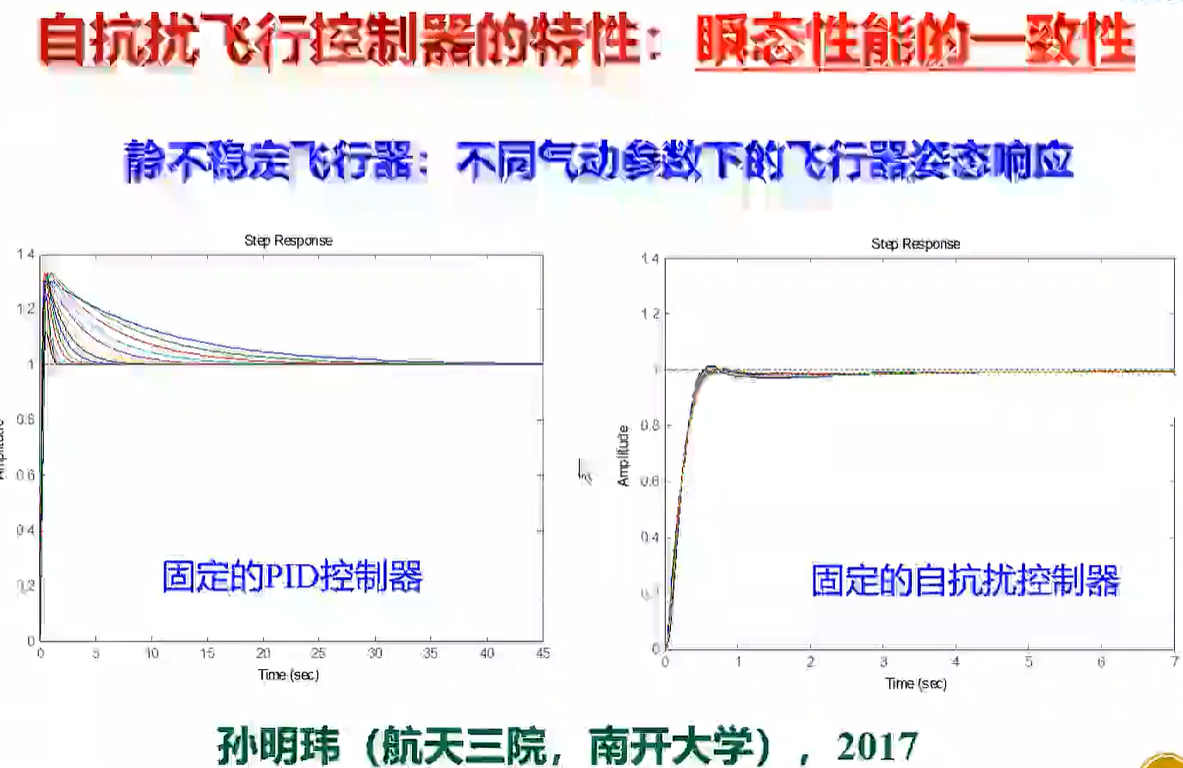
控制器参数不变,ADRC 可以很好地适应系统参数的变化.
3 一般不确定系统的 ESO 设计方法及应用¶

所考虑范围内:指扰动是预期内的,比如正弦,阶跃等
输入和输出是 0, 就能够确定状态为 0
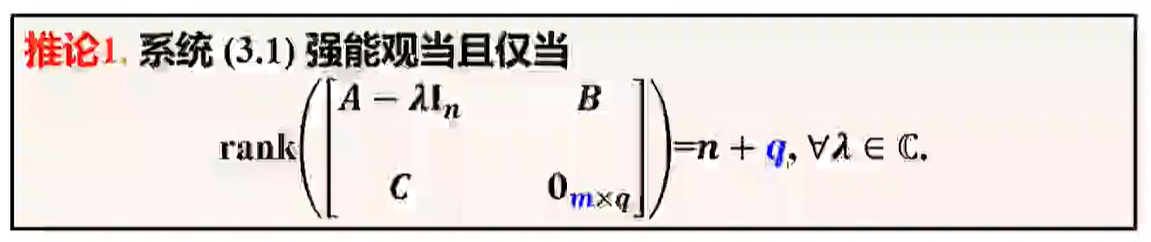
对于系统 (3.1), 扰动维数大于观测维数,则一定不能观

系统状态和扰动的线性组合称为组合状态 v. 如果 v 能观,意味着输出为 0 时,状态组合 v 为 0, 此时可以设计观测器估计 v
… 后面就听不懂了,总之结论: 满足一定条件下,系统可以写成 m 个"积分串联型+总扰动"的表示 (m 为输出维数).

- 把能观的状态组合找到
- 计算输出到输入的相对阶
- 将系统写成积分串联型系统
- 得到系统中总扰动
4 ESO 的强化学习优化调参方法及理论¶

常值带宽
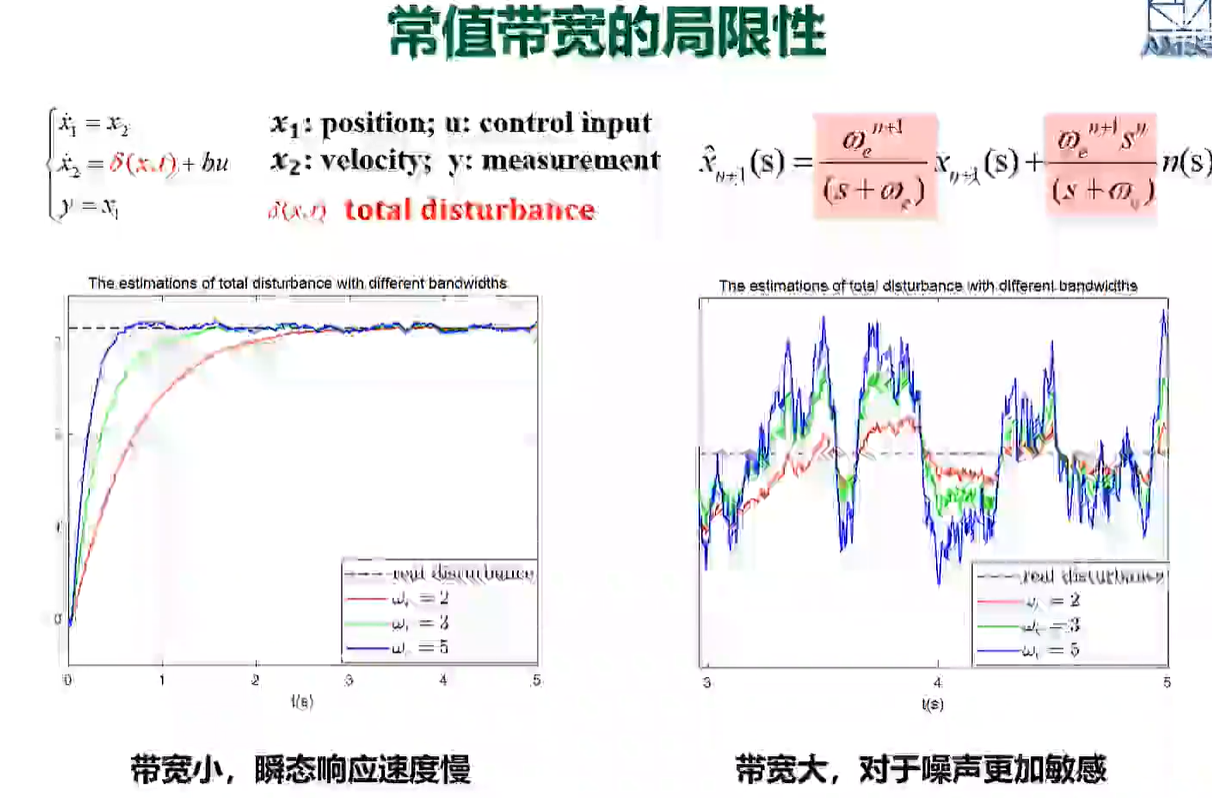

用强化学习的方法在线动态调整带宽。使用输出的估计误差作为评估依据.

5 总结与讨论¶


是否对于任意一个系统都能使用 ADRC 控制,就像 PID 一样?
PID 与 ADRC 都尽量减少对于模型信息的依赖.
PID 很多时候是面对黑箱模型,根据经验之类的进行参数调整.
当然面对白箱也可以很精准地进行调整。
ADRC 应该是对灰箱模型进行控制. 如果面对黑箱,什么信息都不知道,那就是瞎调参数了.. 我们需要知道这个系统最基本的结构,比如说位置、速度、加速度这样的关系,是几阶的,控制增益是多少?