自抗扰控制入门 朱斌¶
1 绪论¶
2 概述¶
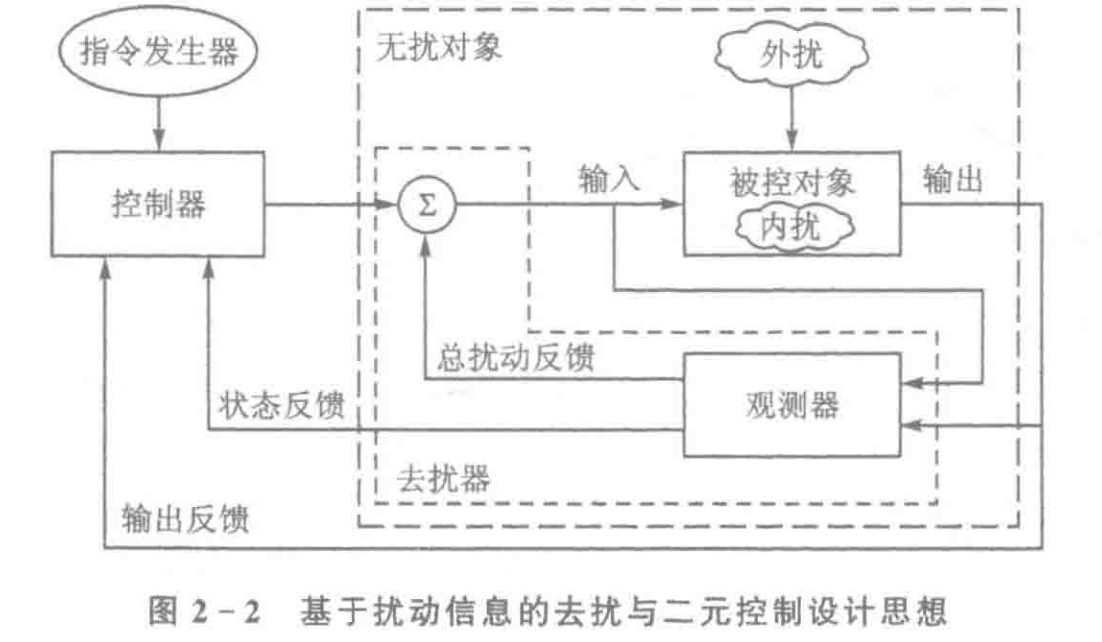
抗扰框架
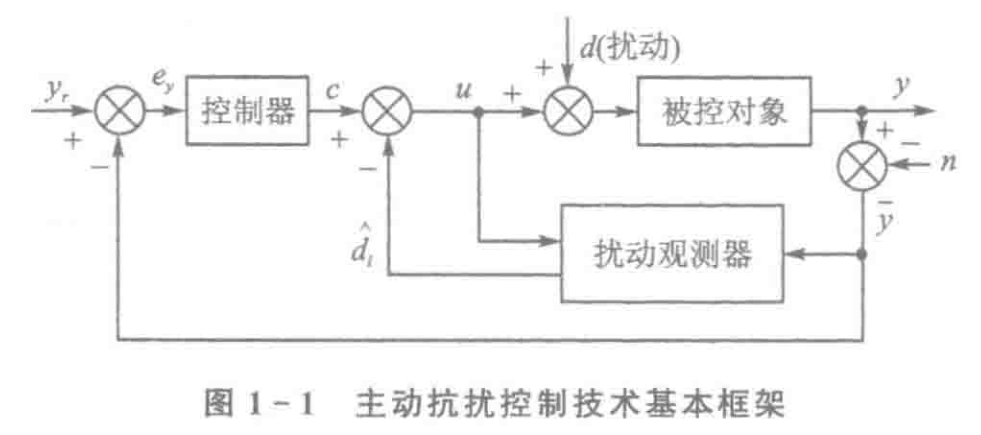
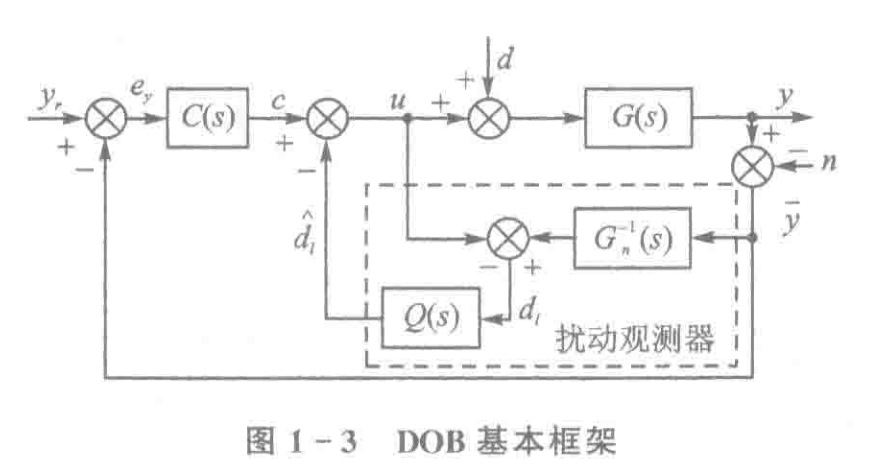
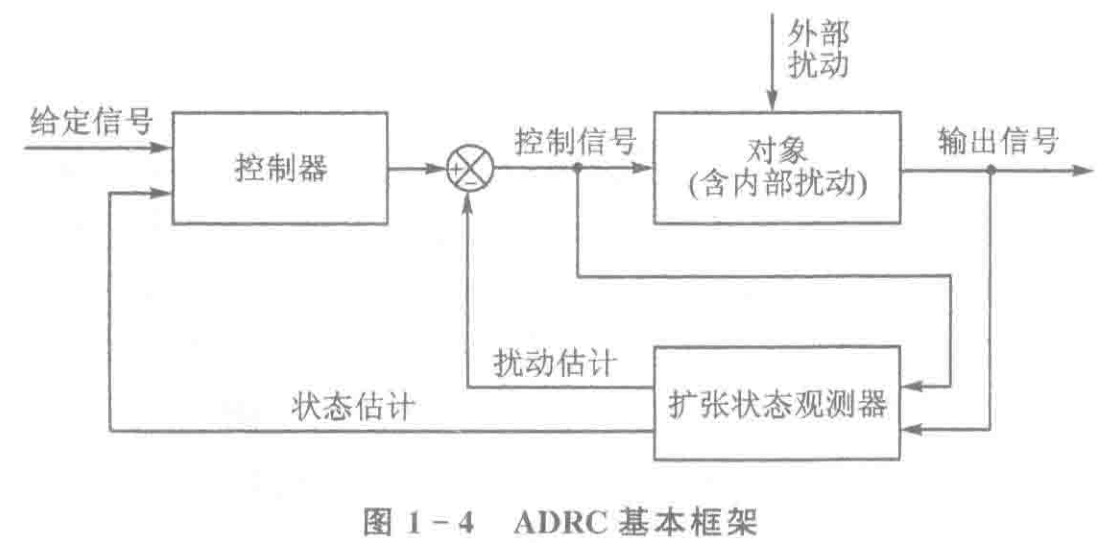
其实结构都差不多,最后被总结成下面的样子.



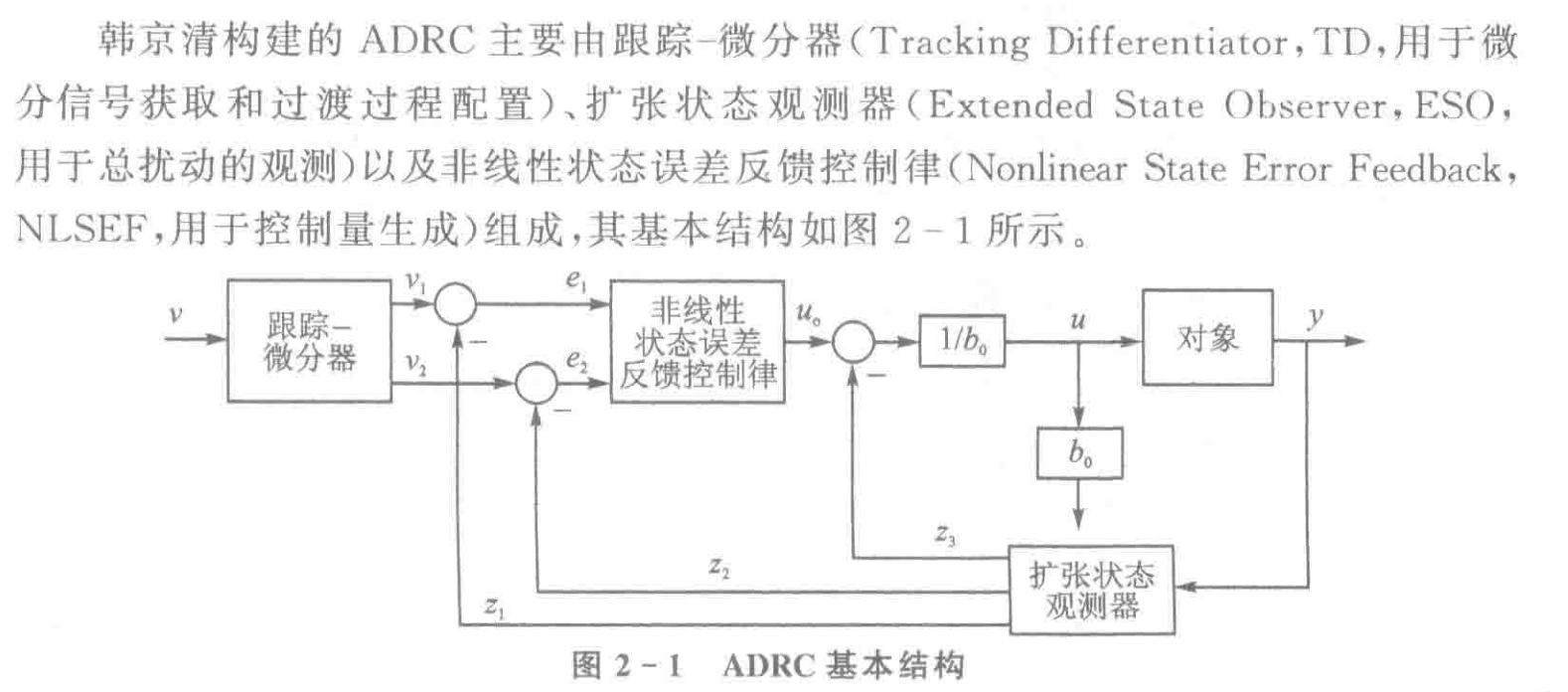


2.1 ADRC 的特性¶
ADRC 需要提前确定:系统的阶数,输入放大系数
当然,如果不知道,通过反复调试,也能找到合适的参数(即便系统阶次变化)

我的理解:
ADRC 关注的是 单输入-单输出 这样的抗扰.
通过 ESO, 将输入输出关系给化成期望的积分串联型.
对于多输入多输出,则是通过分成多个 ADRC 的 单输入-单输出 回路进行控制.

3 核心算法¶
3.1 非线性 ADRC¶
3.1.1 ESO¶
对于系统模型:
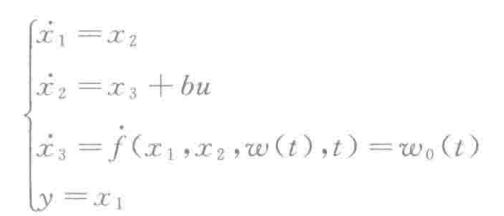
\(x_3\) 是扰动信号, 设立它, 系统变成了线性系统
非线性状态观测器

- z 是观测的 \(\hat x\), 所以 \(\varepsilon_1=\hat y-y\) 实际就是输出误差.
- fal 函数
- \(\delta\) 应该是一个阈值吧, 是一个需要调整的观测器参数
- a 是一个 0.5, 0.25 这样小于1的数
- 总体上, 目的应该是实现小误差大增益, 大误差小增益.
- h 离散步长 (采样周期 T)
3.1.2 TD¶
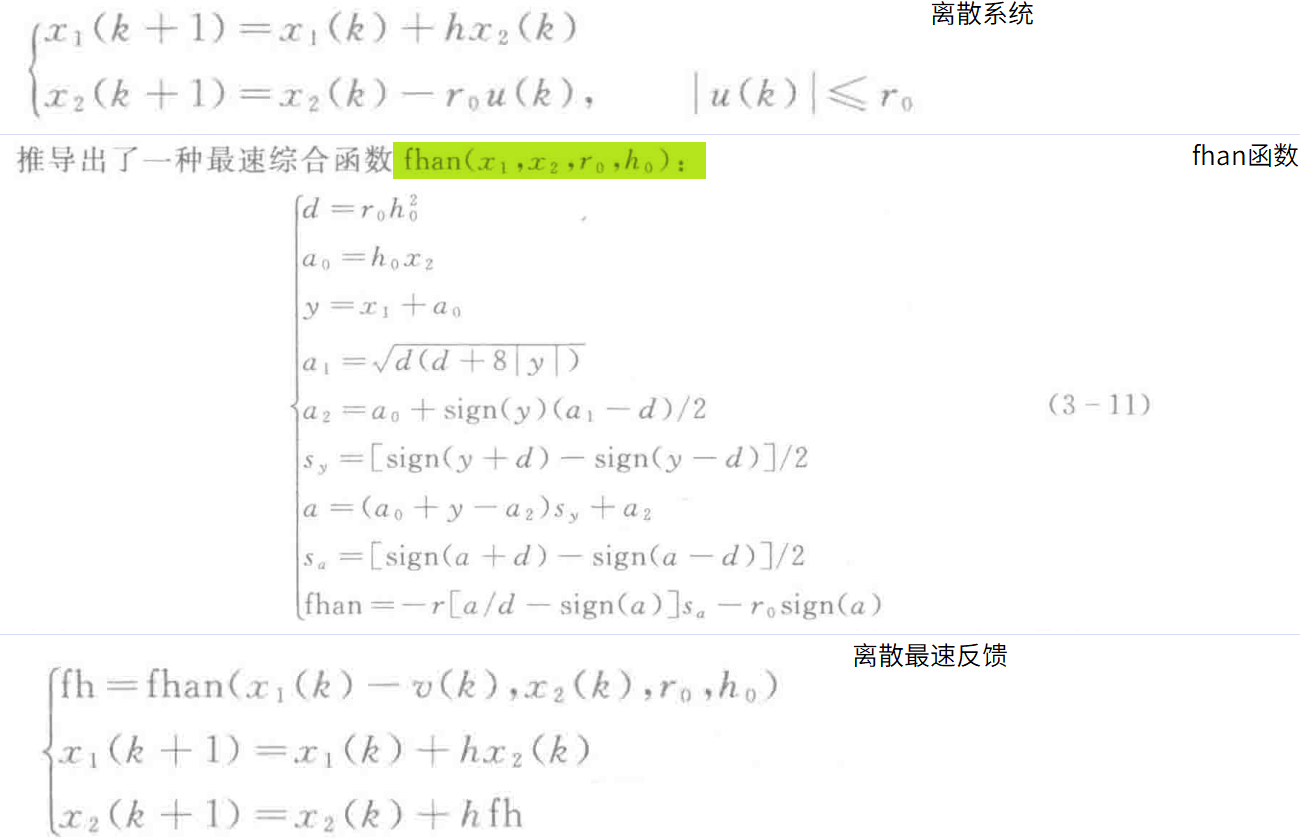
关于最速综合函数:
- 有不同的表达形式
- 最后一行的 \(r\) 应该为 \(r_0\) 费了我好一会…
- \(sign ()\) 是符号函数, 如果为正就是1, 为负就是-1
- 其实可以改成逻辑表达式, 例如 \(s_y=1~\mathrm{if}~|y|<d~\mathrm{else}~ 0\) ,这样更方便理解
离散最速反馈: \(h_0\) 可取为 \(h\) 的若干整数倍
3.1.3 NLSEF¶
通过前面的步骤可以获得误差信号和误差微分信号, 因此可以实现PID (误差的微分, 积分信号线性组合)
扰动可以得到估计和补偿, 所以不需要误差积分信号

3.1.4 U¶

- \(-z_3\) 是补偿扰动
- \(b_0\) 是让参考输入和输出大小相同 (参考输入为1, 输出就为1)
3.1.5 完整算法¶
PDF P33
里面提到了两种算法, 但对比后发现只是表达形式变了, 本质上是一样的, 参数可能变了
3.2 线性 ADRC¶
线性 ADRC 把重点放在观测器, 通过观测器(抗扰器)抵消掉扰动后, 使用什么控制方式都无所谓, 因此可以比较轻松地改进已经设计好的控制系统.
这里使用 PD 控制器对 "二阶串联积分系统" (抗扰后) 进行控制
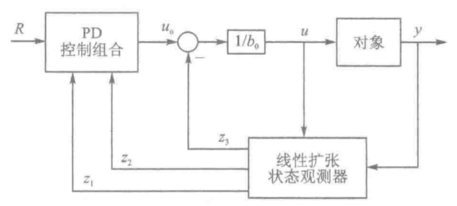
- 跟踪微分器配置过渡过程 → 省略掉
- ESO → 简化为 LESO
- 非线性组合 → 简化 LSEF (大体上是PD控制器)
关于离散化
ADRC 好像并没有太基于状态空间方程之类的, 只是用非线性微分方程组进行表示, 因此离散化只需要将微分方程变成差分方程即可
LADRC 基于线性的状态空间方程进行推导, 因此需要额外推导一下离散后的矩阵 (P46)
3.2.1 系统描述¶
\(y^{(n)}=f+b_0u\)

3.2.2 LESO¶

观测器改进:
- P41 输出直接可测量的情况下, 就不用估计 \(\hat y\) 了
- P43 降阶.
关于观测器带宽 \(\omega_o\) , 意思就是说,(既然线性化了)把观测器极点都配置为 \(-\omega_o\)。 这样观测器的传递函数(大概)就是 \(\frac{1}{(s+\omega_o)^n}\) , 从频域上看, 就是一个低通(???), 之前看到有人说带宽如果足够大, 就能观测到所有扰动.
观测器输出观测到的所有状态变量, 也就是观测到的输出及其导数.
而原系统输出只是\(y=x_1\)
3.2.3 LSEF (线性 PD 组合)¶
由于 ESO 能够实时估计并补偿外部与内部扰动, 因此PID中为消除净差而采用的积分器并不需要;
再简化掉非线性组合; 最终变成了 PD 组合设计

与ADRC不同, 这里忽略了给定值的变化, 即(假定) \(\dot r=0\), 此时控制器实际上就是一个PD控制器
2阶系统, 有一个P,一个D; n阶系统, 有1个P, n-1个D
这里假定经过补偿, 我们的系统变成了 \(\ddot y=bu\) 代入上面的公式, 就可以得到传递函数.
\(\ddot y=f+bu\), 假定已经估计出 \(\hat f=f\), 则\(u_0=k_p(r-y)-k_d\dot y\), 得到控制量 \(u=\frac 1b u_0-\hat f\), 代入原式, 可得理想情况下 \(\ddot y = u_0\) !!!
可以理解成, PD控制器对一个二阶串联积分环节进行调整, 实际上按道理进行推导会有一个零点, 但是这里变成了二阶环节. 是因为这里令 \(\dot r=0\), 而传统的PD仍然是对误差\(e\)求导, 导致闭环传递函数没有零点.
对控制器带宽的理解: PD 控制器把二阶串联积分改造成了二阶环节, 相当于是 -60dB , 也是一个低通.. 这个角度上, 系统最终有一个带宽. (我是这样理解的?)
3.2.4 参数整定¶
P60
LADRC 参数整定比较方便且直观.
只有三个参数: \(\omega_o, \omega_c, b_0\)

\(b_0/b=4\)系统不稳定, 偏离越多, 相角裕度越小; \(\omega_o/\omega_c\) 越大, 相角裕度越高. 两者增加都会使抗噪能力变差.

4 理论分析¶
5 参数整定¶
-
LESO带宽 \(\omega_o\) 增大,有助于LADRC的稳定性和鲁棒性,但过大的 \(\omega_o\) 可能导致控制器输出过大,不利于工程应用,实际调参需要折中
-
对于二阶系统,带宽 \(\omega_o\) 虽然不会影响超调量的大小,但是会影响LESO的跟踪速度,\(\omega_o\)越大,系统响应越快,但是在实际系统中,\(\omega_o\) 的提高受观测噪声等的限制。增大\(\omega_o\) ,同时高频带增益也随之增加,噪声放大作用明显;
-
约定当且仅当系统的状态 \(x_i\) 和LESO跟踪误差 \(\tilde x\)都稳定时,称LADRC系统稳定;
-
假设 \(K_G=b_0/b\), \(K_G\) 偏离1越远,系统相角裕度越小。当 \(K_G=4\) 时,系统不稳定,因此为了改善控制性能,参数 \(b_0\) 的选取应该尽可能接近真实参数 \(b\)
-
实际调试参数时,首先确定系统的阶数N, 其次确定一个Wo, Wc不变(如Wo=50, Wc=20),再按照数量级,依次调试b0, 如0.01, 0.1, 1, 10, 100,…, 直到系统输出满足期望状态;
-
增大带宽会导致系统噪声过大,因此可在LESO前端设置滤波器来抑制其影响;
-
LESO的微分方程的求解,一般依赖初始值(RungeKutta),初值对系统输出的超调量有一定影响;
Wo和Wc的单位都是rad/sec.