Skip to content

CH2. 线性系统的能控性和能观性

能控能观性 ⇒ 最优控制，最优估计

1 能控性

1.1 概念

x 能变，且能任意变，而不是有约束地变

  • 如果有限时间内可以有某一个 u, 使状态从 非零有限点（视为误差）到达状态空间的原点 (0), 则能控.
  • 从相轨迹的角度去理解，能控性是指存在一段相轨迹，起点是原状态位置，终点是期望状态位置.
  • 可控指理论可控，现实系统需考虑物理约束

注释：

  • 分清状态可控与系统可控：系统可控要求当前时刻所有状态可控
  • 对于线性定常连续时间系统，能控等价于能达. 离散系统和时变系统，两者不等价.
  • 非奇异变换不改变能控性 \(\hat Q_c=T^{-1}Q_c\)

Note

能控性：存在控制使状态从某个位置回到零点
能达性：存在控制使状态从零点到达某个位置

1.2 能控性判据

Info

模态判据应该和吉尔伯特判据是一个意思
前者是看的一个 b 站网课上的提法，没好好总结
后者是考研复习资料上的提法

  • 模态判据：如果是对角标准型，A 对角线是特征值，状态之间没有耦合, 则若 B 没有全零行，则状态完全能控. （如果是约当标准型，... 略）

  • 代数判据、秩判据: \(Q_c=[B,AB,A^2B]\) 满秩

    对于多输入系统，\(Q_c\) 不是方阵，列数大于行数，可以任取三列，只要行列式不为零就可以了. 还可以根据 \(r(Q_cQ_c^T)=r(Q_c)\), 与自己的转置相乘后，化成方阵.

  • 吉尔伯特判据：

    • 对应 A 的每个约当块的 B 的分块的最后一行不全为零
    • 若某个特征值存在多于一个约当块，还需要对应 A 的每个相同特征值约当块的 B 的分块的最后一行线性无关. （最后一行全为 0 则线性相关）


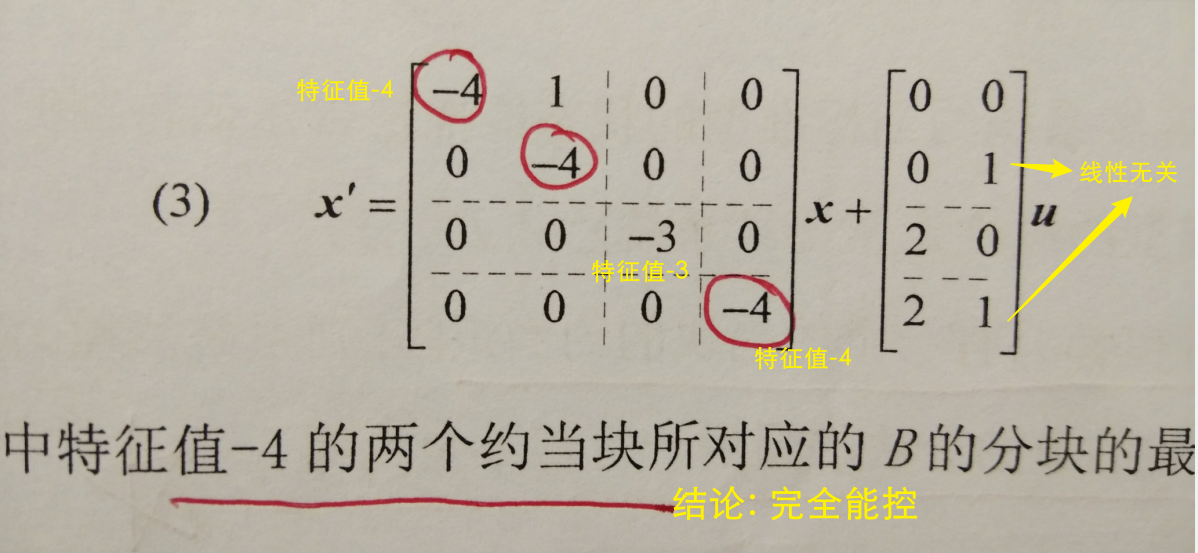
    哪一个特征值对应的约当块出问题，就说明该特征值对应极点不能控.
    对角矩阵每一个对角元素都是一个约当块

  • PBH 判据

能控性判据总结

2 能观性

2.1 概念

有限时间区间内测量 y, 可以唯一确定 \(x_0\)

  • 对于连续时间系统，能观等价于能重构.
  • 非奇异变换不改变能观性. \(\hat Q_o=Q_oT\)

2.2 能观性判据

  • 模态判据：解耦，化成对角标准型（约当标准型）, 输出矩阵 C 不包含全零列（对于约当标准型. 略
  • 代数判据：\(Q_o=[C,CA,CA^2]^T\) 满秩

  • 吉尔伯特判据：

    • 对应 A 的每个约当块的 C 的分块的最第一列不全为零
    • 若某个特征值存在多于一个约当块，还需要对应 A 的每个相同特征值约当块的 C 的分块的第一列线性无关. （第一列全为 0 则线性相关）

    哪一个特征值对应的约当块出问题，就说明该特征值对应极点不能观.
    对角矩阵每一个对角元素都是一个约当块

  • PBH 判据：

能观性判据总结

3 对偶性

\(\sum_1(A,B,C)\leftrightarrow \sum_2(A^T,C^T,B^T)\)

  1. 1 的能控性等价于 2 的能观性，1 的能观性等价于 2 的能控性 （根据代数判据那里进行转换可证明）
  2. 互为对偶系统的传递函数阵互为转置
  3. 特征方程相同，特征值相同 (\(A,A^T\)特征值相同）
  4. 最优控制问题和最优估计问题可以相互转化.

4 系统变换

  • 对于完全能控/完全能观的系统，可以通过线性变换化为能控/能观标准型
  • 对于不完全能控/能观的系统，可以通过线性变换分解为能控子系统和能观子系统.

上述两者其实都是遵循某种步骤对状态空间方程进行线性变换，从而便于后续其他处理. 所以这里放在一起.

步骤对比

4.1 能控标准型和能观标准型

线性系统理论（三）能控和能观标准型 - 知乎 (zhihu.com)

能控标准 I 型，能观标准 II 型

坐标变换 \(X=T\hat X\)

\(\hat A=T^{-1}AT\), \(\hat B=T^{-1}B\), \(\hat C=CT\)

能控标准 I 型 (B 的最后一行是 1)

  1. 求\(Q_c\)满秩则能控
  2. 取\(p_1=[0,0,...,1]Q_c^{-1}\) 最后一行
  3. \(T^{-1}=[p_1,p_1A,...]^{T}\)

能观标准 II 型 (C 的最后一列是 1)

  1. 求\(Q_o\)满秩则能观
  2. 取\(p_1=Q_o^{-1}[0,0,...,1]^T\) 最后一列
  3. \(T=[p_1,Ap_1,...]\)

4.2 线性系统的结构性分解

4.2.1 能控性分解

方法论总结

4.2.2 能观性分解


4.2.3 其他

这部分来自于看的清华大学那个网课，和上面差不多

通过\(X=T\hat X\)进行坐标变换.

  • 能控状态分解：\(r(Q_c)=r<n\) , 选择 r 个线性无关的列作为 T 的前 r 列，再构造剩余 n-r 列，使 T 满秩.

    变换后前 r 列对应能控部分

  • 能观状态分解：\(r(Q_o)=r<n\) , 选择 r 个线性无关的行作为 T 的前 r 行，再构造剩余 n-r 行，使 T 满秩.

  • 卡尔曼分解（略

5 传递函数阵

5.1 定义

线性定常连续系统传递函数阵为 \(G(s)=C(sI-A)^{-1}B+D\)

  • 输入输出间无直接关联项的系统 \(D=0\) （我觉得可以从微分方程输入输出阶数/传递函数分子分母阶数理解，一般分子阶数大于分母阶数）
  • 求传递函数阵则默认零初始状态 \(X(0)=0\)

5.2 结构性分解和零极点相消

对于单输入单输出，传递函数有零极点相消，则不能控或者不能观.

传递函数只反映能控能观部分，能控子系统的传递函数和整体的传递函数相同.

  • \((sI-A)^{-1}B\) 有零极点相消，则相消对应的极点不能控
  • \(C(sI-A)^{-1}\) 有零极点相消，则相消对应的极点不能观

5.3 传递函数的实现问题

Note

其实传递函数就是常系数线性微分方程的一个转换形式，很容易进行互相转换. 所以 微分方程/传递函数 → 状态空间方程，方法可迁移
之所以说是实现问题, 是考虑到传递函数（对于现代控制理论来说）不反应系统的全部信息（不能控/不能观的部分）, 并且由于状态变量选择并非唯一，因此由传递函数写状态空间方程有无数种情况.

传递函数阵的实现问题：传递函数 ⇒ 状态空间方程

  1. SISO 的能控标准型实现：

    • 传递函数一般分母阶数高于分子阶数，如果分子分母同阶，需要先化简成上图形式，多一个 k, 即为 D
    • 只要 G 化简，分子分母没有公因子（没有零极点相消），写出能控标准型，同时也一定能观

  2. SISO 的能观标准型实现：

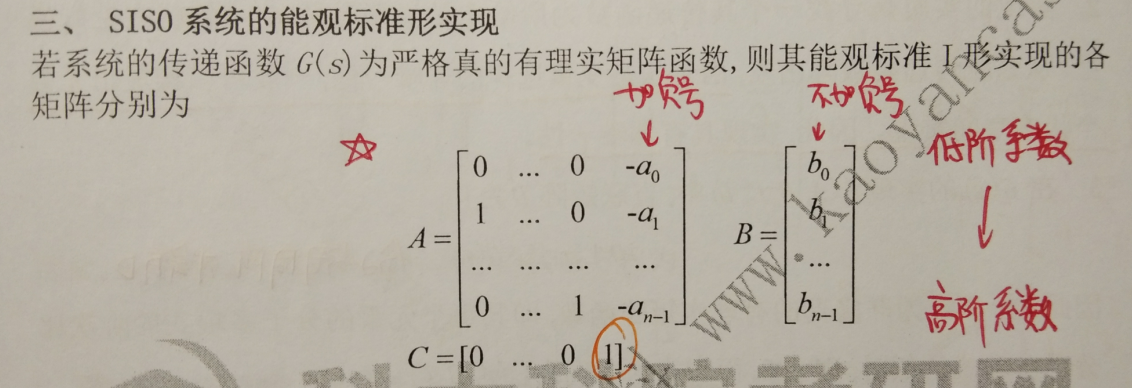
  3. SISO 的约当标准型实现：
    略。..

5.3.1 最小实现问题

最小实现问题：阶数最小、状态变量个数最小
给定传递函数阵的最小实现 \(\Leftrightarrow\) 写出的状态方程完全能控，完全能观

既能控又能观部分与传递函数相对应，阶数是相同的. 不同的最小实现之间代数等价.

多变量系统的最小实现 （清华那个网课记的... 现在不知道在说些什么了）

  1. 卡尔曼方法直接求（略
  2. 先求完全能控，再能观分解，能观子系统就是最小实现.
Back to top