Skip to content

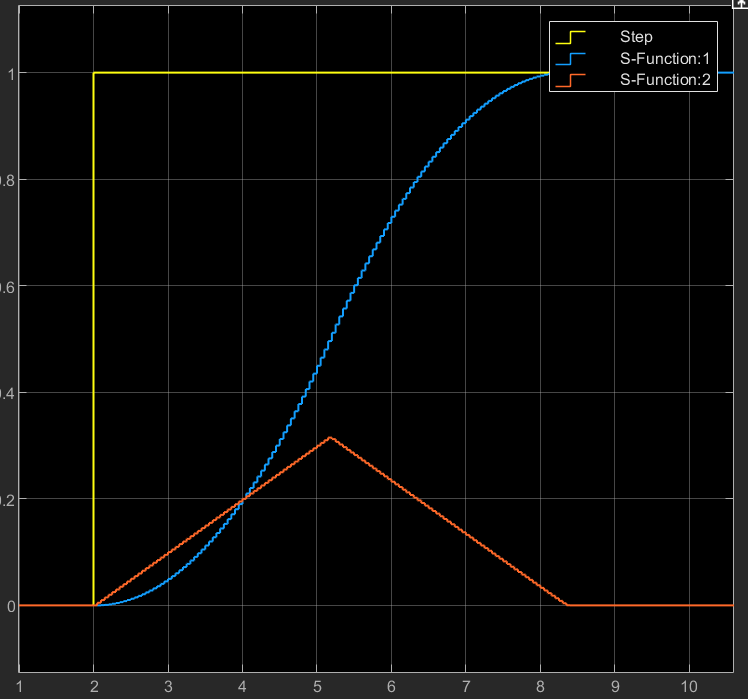
ADRC 调试

一些零散的记录

1 LADRC 调试

\(b\) 值确定:
\(\ddot y=f(\dots)+bu\), 可以由"阶跃响应初始加速度"获得 \(b\)
例如系统 \(\ddot y=-2\dot y-3y+bu\)
原理大致是, 最刚开始 \(\dot y=y=0\), 那么 \(f=-2\dot y-3y=0\)
此时阶跃响应 \(u=1\), \(\ddot y=b\) .

系统离散化后是 \(y(k+2)=−2y(k+1)−3y(k)+bu(k)\)
我们可以直接计算的差分是 \(y(k+1)-y(k)\), 而导数信息应该为 \(\dot y=\frac {y(k+1)-y(k)}{h}\),
同理可以推出二阶导数为 \(\ddot y =\frac{y(k+2)-y(k)}{h^2}\).
阶跃响应最刚开始, \(y(k+2)\) 最先出现变动, \(y(k)=y(k+1)=0\). 代到原式可以有 \(y(k+2)=u(k)\) 这样能够算出来\(b_0=b\).

关于更新


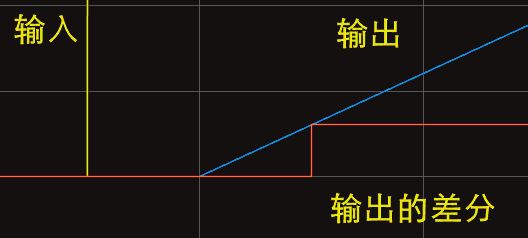
很容易理解, 在 simulink 中, 仿真中数值的更新是一步一步的.
即使搭建连续系统, 计算机最终还是转化成离散的进行一步步更新. 导数阶次越高的最先响应.
对于系统 \(y''=-2y'-3y+u\) , 离散化后是 \(y(k+2)=-2y(k+1)-3y(k)+u(k)\),
肯定是 \(y(k+2)\) 先产生变化, 在那之前 \(y(k+1)=y(k)=0\)

总之:

  • 获取输出的差分, 进而从会变化的最高阶的差分获取到系统阶数以及 \(b\)
    • 虽然理论上说是可以这样测, 但是实际上也可以通过经验试凑…
    • \(b\) 越小, 控制作用越强, 如果\(b\)设置的很小很小, 那么系统的响应又快又没有超调. 但实际系统控制作用是有限的. \(b\) 设置的大到一定程度, 就不稳定了.
  • 阶数取低了好像会不太稳定… 输出不收敛, 阶数取高了我也没试过会发生什么
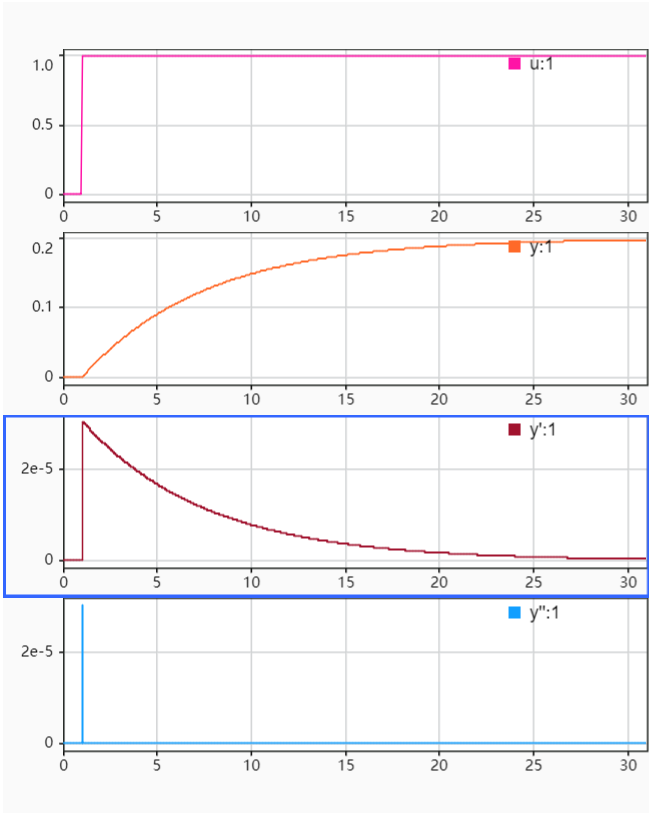
测定 \(\tau_u-u\) 的 \(b\)


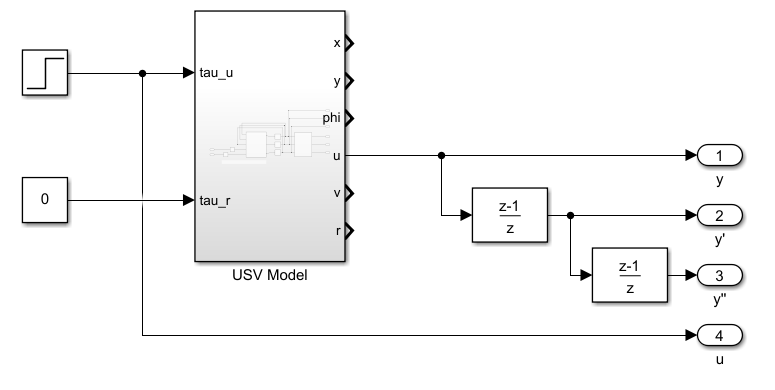
曲线大致为下图: \(y(k+1)-y(k)=3.03e-5\), 表明 \(y'=f+30.3u\), 即 \(\tau_u-u\) 是一阶关系(使用一阶ADRC就可以了)

2 ADRC 调试

TD 配置过渡过程, 有人说是起滤波作用, 对参考值的突变进行平滑处理.
但是这个"过渡过程"的配置也许并不是必须的, 可以根据实际情况自行设定过渡过程.
TD 存在的情况下, 它配置的过程的快慢决定了系统速度的上限.

Back to top