模型编写¶
Summary
控制器/系统编写→把微分/差分方程转化成代码.
(MATLAB) 对于简单的部分, 可以使用图形化方法拖拽链接.
复杂部分图形方法不便组合, 可以使用 S-Function 或者 MATLAB Function.
只需要明确 输入, 输出, 状态变量, 以及状态变量如何更新. 相隔固定周期调用更新函数即可.
1 USV 编写¶
\(m_{11}=m_{22}=33kg,\quad m_{33}=10kg·m^2,\quad m_{23}=m_{32}=3.3kg·m\)
\(d_{11}=d_{22}=d_{33}=5,\quad d_{23}=d_{32}=0\)
考虑到USV螺旋桨的推进能力和转向能力,系统的最大推进力\(F_{max}=100N\)和最大转向力矩\(T_{max}=50N·m\) 1
另外, 建立 \(F_p,F_s\) 和 \(\tau_u,\tau_r\) 的关系时, 需要用到 \(d_y\), 这里取\(d_y=1\). 2 参考上面最大限制, 则可以取左右推力的约束为 \(0\le F\le 50N\).
(回过头来想… 如果是螺旋桨, 反转不就能让力方向相反了嘛? 所以应该是 \(-50\mathrm{N}\le F\le 50\mathrm{N}\) )
主要思路就是把微分方程整理成 \(\dot{x}=\cdots\) 的形式, 然后搭建
- 基本模块搭建: 加入积分器, 积分器输出端是 \(\dot{x}\), 输入端是等号右侧各个信号的和. 无人艇并非线性系统, 因此不能直接使用 simulink 中那个状态方程模块搭建.
- 使用 S-Function 也可以
无人艇模型的输入是\(\tau_u,\tau_r\) (实际是左右推力 \(F_p,F_s\)), 输出是 \(x,y,u,v,r\) 之类的
2 ADRC 编写¶
ADRC 差分方程形式3:

| (子)系统 | 输入 | 输出 |
|---|---|---|
| 整体 | 给定信号,被控系统输出 | 控制量 |
| TD | 给定信号 | 过渡过程(滤波后的给定?)及其微分 |
| ESO | 被控系统输入(即ADRC输出)和输出 | 观测的状态变量 |
| NLSEN | "误差"及其微分 | 组合后的控制量 |
论文4里的形式
基本上是一样的, 只是符号不一样.
Attention
论文中 TD 的参数 \(h_0=h\) , 即 \(h_0\) 和更新步长一致, 但是书上3说可以取为h的若干整数倍, 效果更好, 因此我觉得还是区分开更好.
另外这些参数直接使用似乎效果不太行, 略微修改了一下.
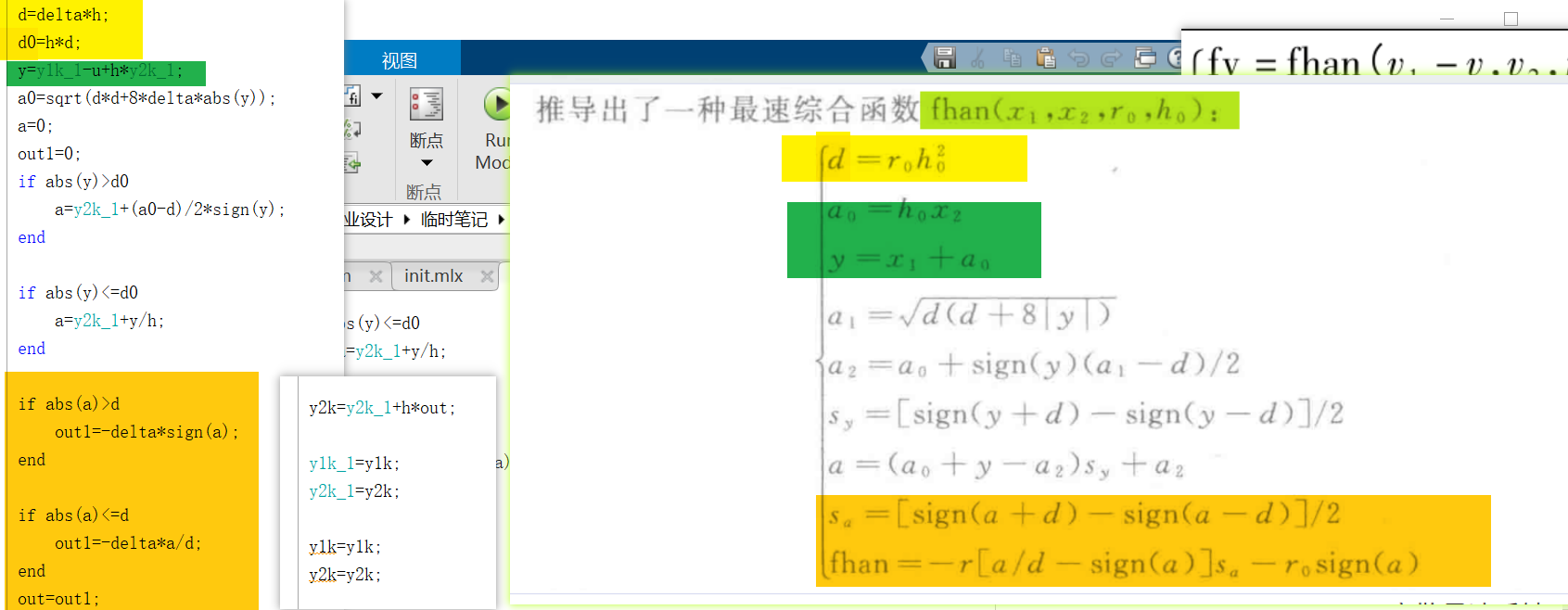
ADRC 的公式可能有其他形式(?), 下图左右略有不同.
左边是别人的ADRC代码